Sonnack.com

A fun way to feel acceleration!

Last time I introduced some of the foundation concepts required for our exploration of Special Relativity. In particular, that the word "special" in this case refers to a specific kind of motion: constant motion in a straight line.

Which may have caused some of you to wonder: Okay, what about motion that isn't constant (and what's that business about "in a straight line" — why keep mentioning that)? As it turns out, when motion involves speeding up, or slowing down, or going along a curve (or even just changing direction), that changes the situation in very significant ways!

That's what I'm going to discuss today.

Albert Einstein introduced his Theory of Special Relativity in 1905. While it involves a brilliant conclusion, most of the background facts were already known at the time. In fact, the ancients knew about the relativity of motion (as I'll discuss next time).

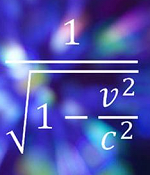The math!

It was Einstein's interpretation of those facts that changed the world.

As I've said before, the math involved is actually fairly simple. The hardest part of the SR equations is a square root. You can calculate the effects of SR using almost any hand calculator.

When you come right down to it, SR takes things that were well-known and looks at them in a — shall we say — special light (I can never resist a punny reference). This new way of looking at things, although quite easy to derive, has some mind-blowing consequences.

Yet it took Einstein 10 years to complete his work on Relativity. He didn't publish his Theory of General Relativity until 1915!

It only took me 10 years!

And that one is much tougher. I'll touch on it a bit down the road, but I won't go into it in much detail. For one thing, the math is above my head. (It involves a mathematical beast called tensors.) But the basics are interesting and worth a look.

I read somewhere once that Einstein didn't want to call his theory one of "Relativity" but of "Equivalence." As we'll see later, SR really is about the equivalence of light to all observers (unlike the motion of physical objects, which differs relative to different observers).

General Relativity (GR) is really about the equivalence of gravity and acceleration — that is, speeding up or slowing down.

When you're in a car that speeds up (either from a stop or from a slower speed), you feel forces that push you back into your seat. When a moving car slows down (to a stop or to a slower speed), you feel forces that seem to push you forward.

It turns out these forces are the same thing — absolutely equivalent to — the force of gravity. In fact, it's really the other way around: gravity is just a form of acceleration. It's exactly the same force you feel when a fast elevator starts moving upwards.

Zero to 60!

I'll come back to this in the future For now I want to focus on acceleration.

When we're standing still (or — more correctly — seemingly standing still relative to our frame of reference), and we start moving, we accelerate from a speed of zero to a speed of… something.

We might measure that speed in miles per hour, or meters per second, or even cubits per nano-jiffy (or one of my personal favorites: furlongs per fortnight), but the point is we go from zero to something (note that speed involves both length units and time units — it's always some length per some time).

If we keep that speed constant — let's say we go from sitting still relative to the road to 60 MPH (96 KPH for many of you) and keep it there — we're no longer accelerating (and now the rules of relativity apply — we can validly say we're motionless and the road is moving past us at 60 MPH).

When we brake to a stop and slow back down to zero; we decelerate — which is negative acceleration.

Feel the acceleration!

The important thing here is that we can feel acceleration. Speeding up seems to push us backward; slowing down seems to push us forward. An instrument, called an accelerometer, can measure the force we feel.

The key here is this: Because we can feel acceleration, we can know that we're moving. And this ruins the symmetry of relative motion!

You might wonder: If gravity is really just acceleration, does that mean we're somehow "moving" even when we're just standing on the ground or sitting in a chair? The answer is: Yes (in a way)!

If not for the floor or the chair, you'd fall towards the center of the Earth. You're feeling the exact same force that pushes you back into your seat when an airplane takes off. If not for the seat, you'd "fall" toward the back of the plane.

'Round and 'round!

Fans of science fiction are well acquainted with the giant spinning wheels used in space stations and space ships to simulate gravity.

If you've ever ridden on one of those carnival rides that spins you around, pinning you to the wall of the ride while the floor drops away, you've experienced rotational acceleration "gravity."

It turns out that, even if your speed is constant, moving in a curve is also a form of acceleration. The force that pushes you against the wall of the carnival ride, or which feels like gravity in a spinning wheel space station, is acceleration.

Any change of speed — speeding up or slowing down — and any change of direction — even at constant speed — is acceleration.

Gravity — no kidding!

And acceleration is a dead giveaway that you're moving.

And when you can tell you're moving, SR does not apply.

Well, it does, but it's no longer the entire picture. You need ten years of intense thought and analysis (and tensors!) to figure out the entire picture because "it's complicated."

Suffice for now to say that general motion is a more challenging situation than special motion. That's why I'm touching only briefly on GR here (and again much later) and focusing almost entirely on SR.

But now you know why it's so important that the motion we're considering is constant (straight line) motion. It's only when we have no feeling of motion that we can think of world speeding past while our car is — seemingly — motionless!

The world speeding past as we just sit there motionless!