SR #25: FTL Drive
 “Engage!” Wait…
“Engage!” Wait…We're finally sliding into home plate in this series (it's baseball season, so I get to use baseball metaphors now). After spending a lot of time looking into how Special Relativity works, we're able to at last explore how it applies to the idea of faster-the-light travel.
Last time we saw that FTL radio seems hopeless — at least at communicating between frames of reference in motion with regard to each other. It's possible there might be a loophole for FTL communication between matched frames. (If nothing else, it may be fertile background for some science fiction.)
Today we examine the idea of FTL motion — of "warp drive!"
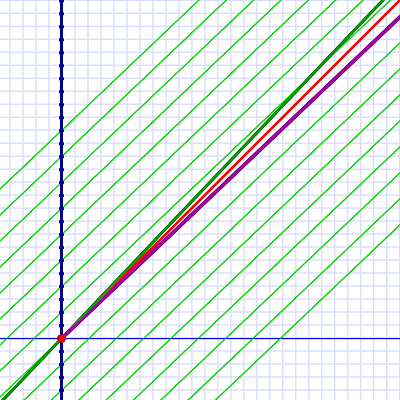
We'll start with this:
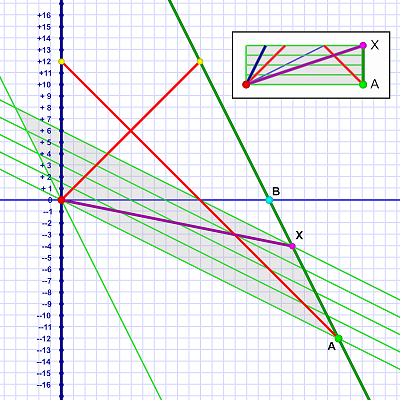
We see Em and her (non-warp!) spacecraft (thick green line) approaching Al and Earth (thick vertical blue line) at a speed of 0.5 c. Some light beams (red lines) show that Al and Em are outside the range of normal communication.
Since Em is in motion (relative to Al), her lines of simultaneity are canted into Al's future. The gray rhombus shape marks out a slice of Em's time that begins for her at event A and ends at event X.
For Al, that slice of time begins at his origin event (the red dot) and ends in his year +6. Note that, for Em, this slice runs from Al's year -12 to Al's year -4 — an eight-year stretch.
This time slice is also shown from Em's POV in the insert to the upper right.
The purple line represents a spacecraft with warp drive traveling from Al's origin point (0x, 0t) to Em's event X.
Note that the flight begins simultaneously with Em's event A (at least from Em's POV). Since event X comes after event A, from Em's point of view, the ship takes off and arrives at her location sometime later.
Other than violating the speed of light law, there's nothing obviously contradictory about the flight from Em's point of view.
But from Al's, the flight clearly takes the ship backwards in (his) time. From his point of view, the flight begins at year 0 and ends at year -4! It seems clear that another flight can be arranged to return to Al prior to the first one leaving — thus creating a causality violation.
So,… let's try a new rule: We can't fly backwards in time relative to the frame we're leaving. ("Change approved!")
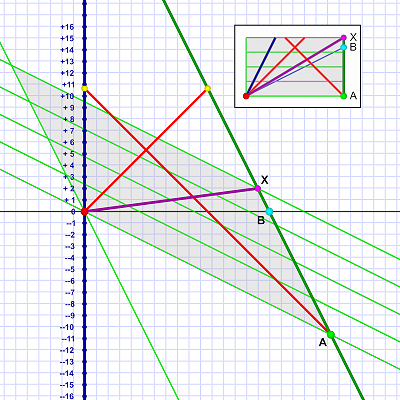
This is nearly the same situation, but we're requiring that the FTL flight from Earth (and Al) not go backwards relative to the launching frame of reference.
The insert in the upper-right again shows the situation from Em's point of view.
This time the flight moves forward in time for both frames of reference. Notice how the flight arrives at event X after Em crosses Al's origin line of simultaneity — the same moment the FTL spacecraft's flight began. The ship arrives after it leaves from both points of view!
So far, so good! We don't seem to be violating causality. Maybe we can pull this off!
The problem is that once the FTL ship arrives at event X, as we saw yesterday with FTL radio, Em can reverse direction to fly away from Al. This rotates her lines of simultaneity the other direction.
Recall that the new rule is the ship can't fly backwards relative to the frame it launches from. As the insert shows, the flight from Em's event A to Al's event X flies forward in time relative to Em's frame. (Note that these events A and X are different from those in the previous diagrams.)
So no problem?
Problem. As you see, the ship now flies backwards in time from Al's point of view. The first leg of the flight began in Al's year 0, but the return flight arrives in his year -3 (bringing with it, sports scores for the next three years).
Oops. We broke the future again.
Okay, so new new rule: FTL drive can't fly backwards in time from either the launching or landing perspectives. ("Change approved!")
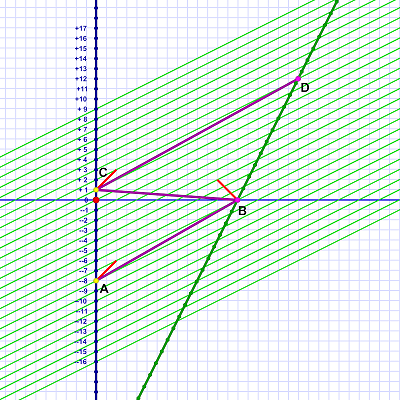
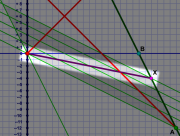
Now we have the situation depicted in diagram 4. I've shown three FTL flights back and forth between Al and Em. As you can see, in Al's frame of reference, the flights from him to Em must go slower to respect Em's lines of simultaneity. (She would, of course, see the situation reversed.)
The flights from Em to Al (again, in Al's frame of reference) seem able to fly much faster. The flight from event B to C, for example, takes only one year in Al's frame, whereas the flight from C to D takes eleven!
Yet, note how the flights to Em, from her point of view, also take only one of Al's years. (They'd actually be even slightly shorter to Em due to time dilation.)
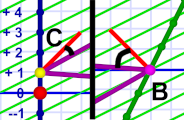 Different angles!
Different angles!Short light beams show how the flights are FTL, but notice how the angle differs between inbound and outbound flights. The outbound flights — due to the need to respect Em's lines of simultaneity — are much closer to the angle (that is, the speed) of light.
This difference in angles seems to signal a problem, since changing to Em's frame of reference would seem to reverse those angles giving two conflicting results.
Worse, why would the frame of reference of the landing point matter? What if the ship's captain changed her mind and landed somewhere else? What if she never landed anywhere?
This seems to suggest that we need yet another new rule that only allows travel that respects all frames of reference. So long as we do that, perhaps we can go as fast as we want?
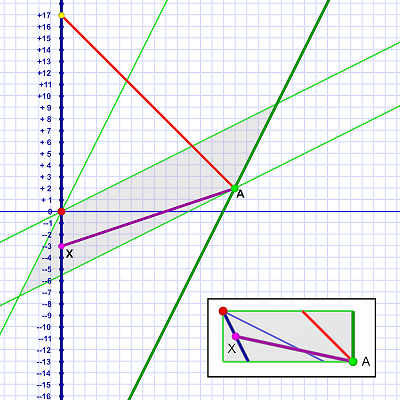
The problem here is that as you approach the speed of light, the angle of your lines of simultaneity and your world line both approach 45 degrees — the angle of the speed of light. Diagram 5 shows Em traveling at 95% of c!
The purple line shows the "FTL" flight allowed given a potential frame of reference at 0.95 c, and as you can see, the angle is very close to the speed of light.
So, a rule that we can only fly as fast as respects all lines of simultaneity up to the speed of light… results in restricting us to (ta da) the speed of light.
 "No FTL for you!"
"No FTL for you!"The bottom line is: Other restrictions involving mass and energy aside, assuming FTL is possible logically leads to the conclusion that it isn't. There is a geometrical necessity to this (showing that, again, Special Relativity is really a geometrical theory based on the consistency of the speed of light).
And that, my dear readers (all three or four of you), is the final punchline of this series — the whole point of it, really. As I said last time: You get…
- Special Relativity
- Causality
- FTL
Pick two.
And now you know why!
This officially concludes this series. I may return to the topic from time to time as the mood strikes me (or if anyone presents questions for which the answer is too long for a comment).
For those who stuck it out through the whole series, congrats! You must have a genuine interest in Special Relativity! And now you should have a pretty good understanding of what it's all about.
As for me, I may take some time off here to catch up on reading and movies (or maybe just napping). See you when I see you!
For future reference, you'll find an index to this series here.