Rotation, Vectors, & Quaternions
This all began with a desire to understand quaternions. Not that I have any particular need for them, but I find rotations in 3D space interesting, which makes quaternions interesting. (At least to me.)
The Complex Plane (it's simple)
To understand quaternions, I think it helps to start with the complex numbers:
c = a + bi
Where c is a complex number, a and b are real numbers, and i is the square root of -1. (While i might bother some, it turns out to be necessary in basic mathematics, and it pops out of that need in a natural way. See: Complex)
This can be treated like:
c = [x, yi]
That is, the two-part complex number can be viewed as a two-dimensional XY coordinate. Which means complex numbers are inherently two-dimensional. To actually plot a complex number, we ignore the i itself and plot the real number parts.
I won't get further into this here; see any math text for details. What matters is that the behavior of i creates an interesting property when it comes to multiplication of two complex numbers.
Specifically, if a complex number is considered as a vector with its tail at the origin, then a complex number also has an angle with respect to the real axis (the X axis). Multiplying complex number C2 by C1 rotates C2's angle by C1's angle. (Assuming C1 is a unit vector; that its magnitude is one.)
Again, this is all basic complex number math. The point is that using the complex plane allows for very easy rotation of points around the origin. Just multiply the points by some unit vector complex number with the desired angle.
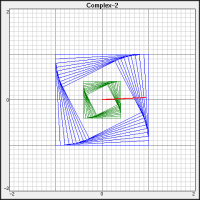
For example, Figure 1 (upper right) shows two boxes (green and blue) that have been rotated by the vector shown as a red line. Note the small angle (only 3°!) the red line forms with the X axis. That's the angle of rotation. Also note how the red line doesn't quite reach the right edge. That's because it's not a unit vector (with length one). It's just shy of length 1.0, so each rotation also “shrinks” the points (i.e brings them closer to the origin). That's why the innermost box is much smaller than the outermost.
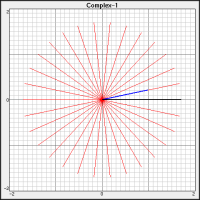
Figure 2 shows this rotation in its simplest form. The rotating line line, this time a unit vector with an angle of 12°, is the blue line. Its coordinates are [cos(12), sin(12)], which results in a unit vector. The black line represents the point being rotated, and the red lines are the rotations.
(The point(s) being rotated can be anything, no requirement for unit vectors. As long as the rotating point is a unit vector, all points rotate at a constant distance from the origin.)
The code is simple and looks like this (note that complex numbers are built in to Python, which makes things much easier):
The rotation angle, ra, is calculated as some number of rotations to make a full circle. The rotation vector, zr, the original vector, z0, and the rotated vector, z1, are all complex numbers. Note that z1 is rotated by simply multiplying it by zr. That's all there is to it!
(The object im is the image object. The vector zc is to represent the origin, [0,0]. The function translate converts complex coordinates to image coordinates.)
Once again, the takeaway is how easy rotations are when using complex numbers. Which brings us to the quaternions…
Quick Detour: The Mandlebrot
BTW, before we move on, the Mandlebrot lives on the same complex plane.
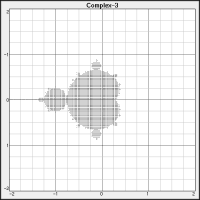
Figure 3 shows my first (very low resolution) attempt to generate it.
It turned out surprisingly well — way better than I expected. I cracked up when it first appeared! Click the image for a higher resolution version that's not bad considering how little effort it took. (It's certainly better than the first published picture (in 1978), which used ASCII art! (See the Wiki article.)
Calculating it is deceptively simple given the amazing results:
That's all there is to the Mandlebrot (well, basically)!
(FWIW, I use the Haskell convention of an 's' suffix meaning a list or collection. IOW, if y is some scalar value, ys is a list of them. Just like if you have a dog, then dogs is a bunch of them.)
Now we can move on to…
Quaternions
If complex numbers let us do interesting things on the complex plane, quaternions let us do interesting things in three-dimensional space.
A quaternion looks like this:
q = a + bi + cj + dk
Where a, b, c, & d, are real numbers, and i, j, & k, are special complex numbers.
At first glance, this might make them seem like four-dimensional numbers. Which they are, strictly speaking. But another way to view them is as a real value plus a three-vector:
q = r + [xi, yj, zk]
The complex numbers give the three-vector some special properties; i.e. the ability to rotate points in 3D space. As with the complex numbers, when actually plotting a quaternion, we ignore i, j, & k, and plot the real numbers, x, y, & z.
Essentially, if a complex number gives us rotation in a plane, then three (interlocked!) rotation planes give us rotations in 3D space.
If you think about how a point in 3D space projects values onto the X, Y, & Z axes, then you can imagine how a rotation in 3-space projects rotations onto X, Y, & Z (complex) planes.[1]
Secret “Magic Sauce”
Now, here's where it gets a little weird, and this might be part of what challenges people about quaternions. It did me, anyway.
The quaterion complex coefficients, i, j, & k, just like the i used in the complex numbers, each have the property that their square is -1.
Specifically:
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | +1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
for quaternion i, j & k. Note
how it does not commute!
ij = k, but ji = -k.
i2 = j2 = k2 = ijk = -1
Now, if you let that sink in, it almost doesn't make sense. One gets — or at least I got — the impression that j and k were just placeholder names for i, that all three were the same thing. That their squares all give -1 sure makes it seem that way.
But it's not that way. They are completely different magic numbers that share properties with the good old i from complex numbers![2]
It may help to understand that these are basis vectors — axes — on different complex planes. It's exactly the same as how X, Y, & Z axes are orthogonal to each other even though they're all represented by real numbers.
So think of i, j & k as three different flavors of “magic sauce” for the X, Y, & Z axes, respectively.
This does complicate quaternion multiplication. Table 1 shows the multiplication table for quaternions, the key feature of which is that multiplication does not commute. (Hopefully, it does compute, though.)
To understand how it works, it's again helpful to start with complex numbers. To multiply two complex numbers, c3 = c1 × c2, we do:
c3 = [a, bi] × [c, di] = ac + adi + bci + bdi2
= ac + (ad + bc)i - bd
= [(ac - bd), (ad + bc)i]
Where a, b, c, & d, are all real numbers.
The trick here is that the i2 resolves to -1, which provides a scalar (which is added to the scalar product). Meanwhile the two terms with i add to provide the “imaginary” part of the new complex number.[3]
![[Quaternion Multiplication]](ijk.png)
Fig. 5: It's a lot easier
to just remember this!
Going against the arrows
gives you a minus result.
So, again:
ij = k, and ji = -k
A similar situation exists when it comes to quaternions. (Only with many more terms and three complex units.) To multiply q1 × q2, we have:
q3 = q1 × q2
= [a1, b1i, c1j, d1k] × [a2, b2i, c2j, d2k]
= a1a2 + a1b2i + a1c2j + a1d2k
+ b1a2i + b1b2ii + b1c2ij + b1d2ik
+ c1a2j + c1b2ji + c1c2jj + c1d2jk
+ d1a2k + d1b2ki + d1c2kj + d1d2kk
Now reduce the i, j, & k, pairs according to the multiplication rules…
q3 = a1a2 + a1b2i + a1c2j + a1d2k
+ b1a2i + b1b2i2 + b1c2k - b1d2j
+ c1a2j - c1b2k + c1c2j2 + c1d2i
+ d1a2k + d1b2j - d1c2i + d1d2i2
And convert any i2, j2, or k2, to -1:
q3 = a1a2 + a1b2i + a1c2j + a1d2k
+ b1a2i - b1b2 + b1c2k - b1d2j
+ c1a2j - c1b2k - c1c2 + c1d2i
+ d1a2k + d1b2j - d1c2i - d1d2
And, finally, collect the like terms:
q3 = (a1a2 - b1b2 - c1c2 - d1d2)
+ (a1b2 + b1a2 + c1d2 - d1c2)i
+ (a1c2 - b1d2 + c1a2 + d1b2)j
+ (a1d2 + b1c2 - c1b2 + d1a2)k
Which I implemented in my Python quaternion class:
(Multiplication by a scalar applies the scalar to each member, as with any vector.)
Quaternion multiplication turns out to be how we rotate points — just as how it is in the complex numbers — so it's necessary to understand how it's done. That said, the final equation above, or the Python code above, can be used as a “recipe” to accomplish it without taking the long way around.
And, as is apparent in the Python code, from a using quaternions to rotate objects perspective, the i, j, & k, are just placeholders for us.
Quick Detour: Real, Complex, Quaternion, Octonion
Quaternions have all sorts of wonderful mathematical properties (that are utterly beyond me), and they apparently have a strong connection with Special Relativity. They're part of a progression of types of numbers we find useful in the real world. The natural numbers (ℕ), the integers (ℤ), and the rationals (ℚ), got us started with analyzing stuff. And…
- The reals (ℝ) are necessary to do any science.
- The complex numbers (ℂ) are necessary in physics.
- The quaternions (ℍ) are useful in SR.
- The octonions (𝕆) might be useful in quantum physics.
What's fascinating is that the four items listed are the only division algebras. Each new type of number adds interesting properties, but each also loses something:
- The real numbers aren't tamed by algebra (because of transcendental numbers).
- The complex numbers aren't ordered (you can't sort multi-dimensional numbers).
- The quaternions aren't communitive (a×b ≠ b×a).
- The octonions aren't even associative ([a×b]×c ≠ a×[b×c]).
But what interested me — and which might interest a lot of programmers — is this: How the heck do you rotate something with a quaternion?
Rotating With Quaternions
Well, I'll tell you! That is, I can tell you how to make it work; I finally figured out how to cast the spells. But I have absolutely no clue as to exactly why it works — I'm a programmer, not a mathematician. Damnit.
The short (unhelpful (but bear with me)) version (also the bottom line) goes like this:
P' = Q × P × Q-1
P' is the result of rotating P, the point we want to rotate. Note that P, an [x,y,z] coordinate, is expressed as the quaternion: [0, xi, yj, zk]. And remember that the i, j, & k are just there to remind us about the magic sauce.
Q is the rotation quaternion, and Q-1 is its inverse.
Honestly, it was confusing descriptions of this process that made it hard for me to figure out. At least, I was confused. To some extent, it was all the extra information that made it hard to absorb the key aspects. Once I sorted through all the stuff real mathematicians need to know about quaternions, it turned out to be fairly simple.
It really does boil down to sticking your [x,y,z] coordinate into a quaternion with its real part set to zero. And all you do is multiply the rotation quaternion by your point quaterion and then by the inverse of the rotation guy. The resulting quaternion has the new [x,y,z] in its vector part. Easy Peasy.
Part of the trick is that rotation quaternion and its inverse.
First, pick your rotation vector. IOW, pick some [x,y,z] that, as a vector, is your rotation axis. Then, pick a rotation angle. That's how much you want to rotate whatever you're rotating.
As a simple example, assume we want to spin something like a top, about its vertical axis.[4] And let's say we want to rotate it five degrees (5°).
The unit vector here is simple, it's just [0,1,0]. If we wanted a less orthogonal angle, let's say [+10,-3,+5], we'd need to take the unit vector of that, which is [+0.864, -0.259, +0.432]. (If we want to think in terms of angles, it can be a little more complicated — but not too bad, just some trig.[5])
We create a rotation quaternion like this:
Qrot = [cos(θ/2),Vxsin(θ/2),Vysin(θ/2), Vzsin(θ/2)]
Where Q is the rotation quaternion, V is the rotation vector, and θ is the rotation angle.
For our “spin like a top” example, the rotation quaternion looks like:
Qrot = [+0.999048, +0.0, +0.043619, +0.0]
The rotation quaternion for the second example looks like this:
Qrot = [+0.999048, +0.037681, -0.011304, +0.018841]
We also need Qrot-1, the inverse, or reciprocal, of Qrot.
For quaternions, this is defined as: Q* ÷ |Q|2.
That is, the complex conjugate of Q (notated as Q*) divided by the squared norm (aka magnitude, notated as |Q|).[6]
Note that we're dividing the vector, Q*, by a scalar here, which results in a new vector. (The inverse of a quaternion is a quaternion.)
The complex conjugate of a quaternion, as with a complex number, just inverts the complex parts. For a quaternion, Q* = [a, -bi, -cj, -dk].
(Again, the i, j, & k are just placeholder reminders. In reality, a–d are real numbers.) The bottom line is that:
Qrot-1 = [+0.999048, -0.0, -0.043619, -0.0]
…and (second example)…
Qrot-1 = [+0.999048, -0.037681, +0.011304, -0.018841]
Now all we do is carry out the multiplication:
P' = Q × P × Q-1
For any and all points we want to rotate.
In Python, given quaterion and vector classes, it can look as simple as this:
qs = [qr * q * qr.recip() for q in qs]
Where qs is a list of (quaternion) points to rotate, and qr is the rotation quaternion.
The inverse (reciprocal) comes from the quaternion recip() method.
Here is the Python code implementing the necessary methods:
The Code
[1] This may be completely wrong. I am not a maths guy — I'm just fascinated by it. And it makes sense to me this way, so whatever.
[2] Focus on the ijk = -1 part to see they must be different, because iii = i2i = -1i = -i. In fact, both the multiplication table (Table 1) and the circular diagram (Figure 5) can be derived from ijk = -1.
[3] I agree with mathematicians who (in some cases, intensely) dislike the term "imaginary" for wonderful and totally real i. Therefore, I never use the term "imaginary numbers" — they're called complex numbers — and the second part is called the complex part.
[4] The coordinate system follows a left-handed rule: The left thumb and next two fingers are, respectively, X, Y, & Z, and point in the positive direction. The index finger, Y, is the vertical axis, pointing up. X and Z are horizontal, with the thumb, X, pointing right and the middle finger, Z, pointing away. Rotation, however, is right-handed; if thumb points in positive direction, fingers point to positive rotation.)
[5]
Say we're Picard and we tell our helmsman to set course to “ 300 mark 40” — that is, 30° forward of left and 40° upwards.
(This assumes azimuth right is 90° (and +X) while azimuth left is 270° (and -X). Forward is +Z.)
After adjusting azimuth…
angle = ((450-azimuth) % 360)
…we have:
[cos(angle), sin(elevation), sin(angle)]
[cos(150), sin(40), sin(150)]
Which gives us the unit vector:
[-0.729, +0.541, +0.421]
[6] In the reals, |r| means the absolute value of r. But with vectors, |v| means the magnitude (length) of v, and is calculated as the square root of the sum squares of the members. The same magnitude concept in quaternions is called the norm and is usually notated ||q|| (rather than just |q|). Don't ask me why. Since they are the same concept, I've notated it using just |q|. But technically I suppose it's wrong.
[*] OMG: How many times does the word "quaternion" apppear in this! I'm so tired of typing it!