LaTeX Equations

x
""
|
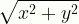
\displaystyle\sqrt{x^2+y^2}
_
|
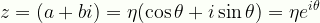
\displaystyle{z}=(a+bi)=\eta(\cos\theta+{i}\sin\theta)=\eta{e}^{i\theta}
complex1
|

\displaystyle\eta=|z|=\sqrt{a^2+b^2},\;\;\;\theta=\arg(z)=\arctan\frac{a}{b}
complex2
|
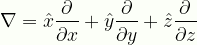
\displaystyle\nabla=\hat{x}\frac{\partial}{\partial{x}}+\hat{y}\frac{\partial}{\partial{y}}+\hat{z}\frac{\partial}{\partial{z}}
nabla
|

\displaystyle\nabla^2=\hat{x}\frac{\partial^2}{\partial{x^2}}+\hat{y}\frac{\partial^2}{\partial{y^2}}+\hat{z}\frac{\partial^2}{\partial{z^2}}
nabla2
|
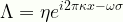
\displaystyle\Lambda=\eta{e}^{{i}2\pi\kappa{x}-\omega\sigma}
sine1
|
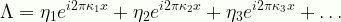
\displaystyle\Lambda=\eta_1{e}^{{i}2\pi\kappa_1{x}}+\eta_2{e}^{{i}2\pi\kappa_2{x}}+\eta_3{e}^{{i}2\pi\kappa_3{x}}+\ldots
sine2
|
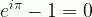
\displaystyle{e}^{{i}\pi}-1=0
Euler
|
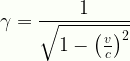
\displaystyle\gamma=\frac{1}{\sqrt{1-\left(\frac{v}{c}\right)^2}}
Lorentz
|
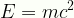
\displaystyle{E}={mc}^{2}
SR1
|
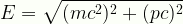
\displaystyle{E}=\sqrt{(mc^{2})^{2}+(pc)^{2}}
SR2
|

\displaystyle{G}_{\mu\nu}+\Lambda{g}_{\mu\nu}=\frac{8\pi{G}}{c^4}T_{\mu\nu}
GR
|

\displaystyle{T}={2}\pi\sqrt{\frac{{a}^{3}}{GM}}
orb.period
|

\displaystyle{v}\approx\sqrt{\frac{GM}{a}}\;\;\;\textsf{note:}\;{GM}=\mu
orb.speed1
|
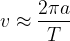
\displaystyle{v}\approx\frac{{2}\pi{a}}{T}
orb.speed2
|

\displaystyle{a}=\sqrt[3]{\frac{GMT^2}{{4}\pi^{2}}}
orb.radius
|
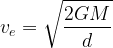
\displaystyle{v}_{e}=\sqrt{\frac{{2}GM}{d}}
esc.speed
|
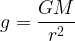
\displaystyle{g}=\frac{GM}{{r}^{2}}
surf.grav
|
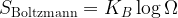
\displaystyle{S}_\text{Boltzmann}={K}_{B}\log\Omega
entropyB
|
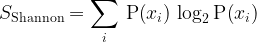
\displaystyle{S}_\text{Shannon}=\sum_{i}\,\text{P}\!\left({x}_{i}\right)\,\log_{2}\text{P}\!\left({x}_{i}\right)
entropyS
|

\displaystyle\frac{\partial}{\partial{t}}\,{T}(x,\!t)={D}\frac{\partial^{2}}{\partial{x}^{2}}\,{T}(x,\!t)
diffusion
|

\displaystyle{g}(x,y)={ae}^{-\left(\frac{x^2+y^2}{c^2}\right)}
Gauss2
|

\displaystyle{g}_x'(x,y)=\frac{\partial}{\partial{x}}{ae}^{-\left(\frac{x^2+y^2}{c^2}\right)}=\frac{-2ax}{c^2}\;{e}^{-\left(\frac{x^2+y^2}{c^2}\right)}
Gauss2dx
|
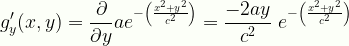
\displaystyle{g}_y'(x,y)=\frac{\partial}{\partial{y}}{ae}^{-\left(\frac{x^2+y^2}{c^2}\right)}=\frac{-2ay}{c^2}\;{e}^{-\left(\frac{x^2+y^2}{c^2}\right)}
Gauss2dy
|
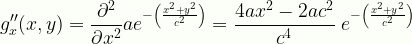
\displaystyle{g}_x''(x,y)=\frac{\partial^2}{\partial{x^2}}{ae}^{-\left(\frac{x^2+y^2}{c^2}\right)}=\frac{4ax^2-2ac^2}{c^4}\;{e}^{-\left(\frac{x^2+y^2}{c^2}\right)}
Gauss2dx2
|

\displaystyle{g}_y''(x,y)=\frac{\partial^2}{\partial{y^2}}{ae}^{-\left(\frac{x^2+y^2}{c^2}\right)}=\frac{4ay^2-2ac^2}{c^4}\;{e}^{-\left(\frac{x^2+y^2}{c^2}\right)}
Gauss2dy2
|
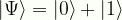
\displaystyle|\Psi\rangle=|0\rangle+|1\rangle
Q1
|
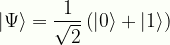
\displaystyle|\Psi\rangle=\frac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)
Q2
|
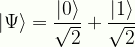
\displaystyle|\Psi\rangle=\frac{|0\rangle}{\sqrt{2}}+\frac{|1\rangle}{\sqrt{2}}
Q3
|
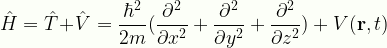
\displaystyle\hat{H}=\hat{T}\!+\!\hat{V}=\frac{\hbar^2}{2m}(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2})+V(\bold{r},t)
Hamilton
|

\displaystyle{i}\hbar\frac{d}{dt}\,\Psi(x,\!t)=\hat{H}\,\Psi(x,\!t)
Schrod1
|
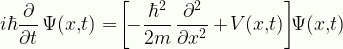
\displaystyle{i}\hbar\frac{\partial}{\partial{t}}\,\Psi(x,\!t)=\!\left[\!-\frac{\hbar^2}{2m}\,\frac{\partial^2}{\partial{x}^2}+\!V(x,\!t)\right]\!\!\Psi(x,\!t)
Schrod2
|
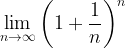
\displaystyle\lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^{n}
Expon0
|
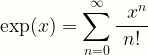
\displaystyle\exp(x)=\sum_{n=0}^{\infty}\frac{\;\;x^n}{n!}
Expon1
|
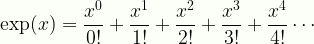
\displaystyle\exp(x)=\frac{x^0}{0!}+\frac{x^1}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}\cdots
Expon2
|

\displaystyle\exp(x)=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}\cdots
Expon3
|
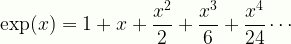
\displaystyle\exp(x)=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}\cdots
Expon4
|
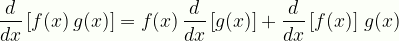
\displaystyle\frac{d}{dx}\left[f(x)\,g(x)\right]=f(x)\,\frac{d}{dx}\left[g(x)\right]+\frac{d}{dx}\left[f(x)\right]\,g(x)
product
|
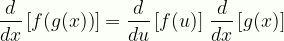
\displaystyle\frac{d}{dx}\left[f(g(x))\right]=\frac{d}{du}\left[f(u)\right]\,\frac{d}{dx}\left[g(x)\right]
chain
|
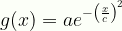
\displaystyle{g}(x)={ae}^{-\left(\frac{x}{c}\right)^2}
Gauss1
|
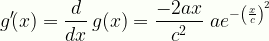
\displaystyle{g}'\!(x)=\frac{d}{dx}\,{g}(x)=\frac{-2ax}{c^2}\;{ae}^{-\left(\frac{x}{c}\right)^2}
Gauss1dx
|
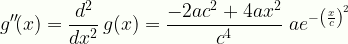
\displaystyle{g}''\!(x)=\frac{d^2}{dx^2}\,{g}(x)=\frac{-2ac^2+4ax^2}{c^4}\;{ae}^{-\left(\frac{x}{c}\right)^2}
Gauss1dx2
|

\displaystyle{g}'''\!(x)=\frac{d^3}{dx^3}\,{g}(x)=\frac{-8ax^{3}+12ac^{2}x}{c^6}\;{ae}^{-\left(\frac{x}{c}\right)^2}
Gauss1dx3
|
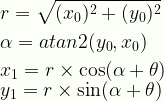
\displaystyle{r}=\sqrt{(x_0)^2+(y_0)^2}\\[6pt]\alpha=atan2(y_0,x_0)\\[6pt]x_1=r\times\cos(\alpha+\theta)\\y_1=r\times\sin(\alpha+\theta)
rot1
|
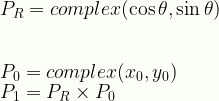
\displaystyle{P}_{R}=complex(\cos\theta,\sin\theta)\\[16pt]\\P_0 = complex(x_0, y_0)\\P_1 = P_R \times P_0
rot2
|
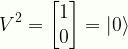
\displaystyle{V}^{2}=\begin{bmatrix}{1}\\{0}\end{bmatrix}=|{0}\rangle
V2C
|

\displaystyle{V}^{3}=\begin{bmatrix}{1}\\{0}\\{0}\end{bmatrix}=|{0}\rangle
V3C
|
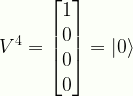
\displaystyle{V}^{4}=\begin{bmatrix}{1}\\{0}\\{0}\\{0}\end{bmatrix}=|{0}\rangle
V4C
|

\displaystyle{V}^{2}=\begin{bmatrix}{1}&{0}\end{bmatrix}=\langle{0}|
V2R
|

\displaystyle{V}^{3}=\begin{bmatrix}{1}&{0}&{0}\end{bmatrix}=\langle{0}|
V3R
|

\displaystyle{V}^{4}=\begin{bmatrix}{1}&{0}&{0}&{0}\end{bmatrix}=\langle{0}|
V4R
|
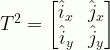
T^2 = \displaystyle\begin{bmatrix}\hat{i}_{x}&\hat{j}_{x}\\\hat{i}_{y}&\hat{j}_{y}\end{bmatrix}
T2
|
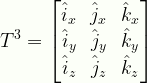
T^3 = \displaystyle\begin{bmatrix}\hat{i}_{x}&\hat{j}_{x}&\hat{k}_{x}\\\hat{i}_{y}&\hat{j}_{y}&\hat{k}_{y}\\\hat{i}_{z}&\hat{j}_{z}&\hat{k}_{z}\end{bmatrix}
T3
|
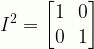
I^2 = \displaystyle\begin{bmatrix}{1}&{0}\\{0}&{1}\end{bmatrix}
I2
|
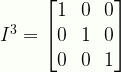
I^3 = \displaystyle\begin{bmatrix}{1}&{0}&{0}\\{0}&{1}&{0}\\{0}&{0}&{1}\end{bmatrix}
I3
|

I^4 = \displaystyle\begin{bmatrix}{1}&{0}&{0}&{0}\\{0}&{1}&{0}&{0}\\{0}&{0}&{1}&{0}\\{0}&{0}&{0}&{1}\end{bmatrix}
I4
|

\displaystyle{R}^{2}_{xy}(\theta)=\begin{bmatrix}{+\cos\theta}&{-\sin\theta}\\{+\sin\theta}&{+\cos\theta}\end{bmatrix}
R2xy
|

\displaystyle{R}^{2}_{xy}({0}^{\circ}) =\begin{bmatrix}{+1}&{0}\\{0}&{+1}\end{bmatrix}
R2xy0
|
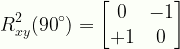
\displaystyle{R}^{2}_{xy}({90}^{\circ}) =\begin{bmatrix}{0}&{-1}\\{+1}&{0}\end{bmatrix}
R2xy90
|
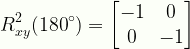
\displaystyle{R}^{2}_{xy}({180}^{\circ})=\begin{bmatrix}{-1}&{0}\\{0}&{-1}\end{bmatrix}
R2xy180
|
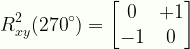
\displaystyle{R}^{2}_{xy}({270}^{\circ})=\begin{bmatrix}{0}&{+1}\\{-1}&{0}\end{bmatrix}
R2xy270
|

\displaystyle{R}^{2}_{xy}({15}^{\circ})=\begin{bmatrix}{+0.96592}&{-0.25881}\\{+0.25881}&{+0.96592}\end{bmatrix}
R2xy15
|
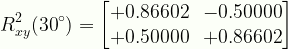
\displaystyle{R}^{2}_{xy}({30}^{\circ})=\begin{bmatrix}{+0.86602}&{-0.50000}\\{+0.50000}&{+0.86602}\end{bmatrix}
R2xy30
|

\displaystyle{R}^{2}_{xy}({45}^{\circ})=\begin{bmatrix}{+0.70711}&{-0.70711}\\{+0.70711}&{+0.70711}\end{bmatrix}
R2xy45
|

\displaystyle{R}^{2}_{xy}({60}^{\circ})=\begin{bmatrix}{+0.50000}&{-0.86602}\\{+0.86602}&{+0.50000}\end{bmatrix}
R2xy60
|
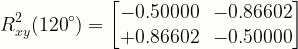
\displaystyle{R}^{2}_{xy}({120}^{\circ})=\begin{bmatrix}{-0.50000}&{-0.86602}\\{+0.86602}&{-0.50000}\end{bmatrix}
R2xy120
|
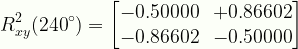
\displaystyle{R}^{2}_{xy}({240}^{\circ})=\begin{bmatrix}{-0.50000}&{+0.86602}\\{-0.86602}&{-0.50000}\end{bmatrix}
R2xy240
|
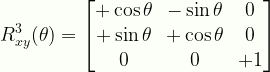
\displaystyle{R}^{3}_{xy}(\theta)=\begin{bmatrix}{+\cos\theta}&{-\sin\theta}&{0}\\{+\sin\theta}&{+\cos\theta}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xy
|

\displaystyle{R}^{3}_{xy}(0^{\circ}) =\begin{bmatrix}{+1}&{0}&{0}\\{0}&{+1}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xy0
|

\displaystyle{R}^{3}_{xy}(90^{\circ}) =\begin{bmatrix}{0}&{-1}&{0}\\{+1}&{0}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xy90
|
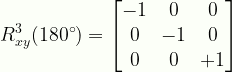
\displaystyle{R}^{3}_{xy}(180^{\circ})=\begin{bmatrix}{-1}&{0}&{0}\\{0}&{-1}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xy180
|

\displaystyle{R}^{3}_{xy}(270^{\circ})=\begin{bmatrix}{0}&{+1}&{0}\\{-1}&{0}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xy270
|
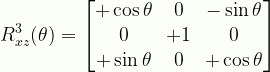
\displaystyle{R}^{3}_{xz}(\theta)=\begin{bmatrix}{+\cos\theta}&{0}&{-\sin\theta}\\{0}&{+1}&{0}\\{+\sin\theta}&{0}&{+\cos\theta}\end{bmatrix}
R3xz
|
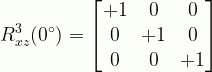
\displaystyle{R}^{3}_{xz}(0^{\circ}) =\begin{bmatrix}{+1}&{0}&{0}\\{0}&{+1}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3xz0
|
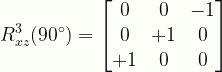
\displaystyle{R}^{3}_{xz}(90^{\circ}) =\begin{bmatrix}{0}&{0}&{-1}\\{0}&{+1}&{0}\\{+1}&{0}&{0}\end{bmatrix}
R3xz90
|

\displaystyle{R}^{3}_{xz}(180^{\circ})=\begin{bmatrix}{-1}&{0}&{0}\\{0}&{+1}&{0}\\{0}&{0}&{-1}\end{bmatrix}
R3xz180
|
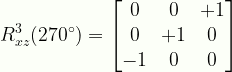
\displaystyle{R}^{3}_{xz}(270^{\circ})=\begin{bmatrix}{0}&{0}&{+1}\\{0}&{+1}&{0}\\{-1}&{0}&{0}\end{bmatrix}
R3xz270
|
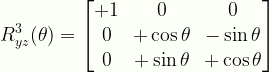
\displaystyle{R}^{3}_{yz}(\theta)=\begin{bmatrix}{+1}&{0}&{0}\\{0}&{+\cos\theta}&{-\sin\theta}\\{0}&{+\sin\theta}&{+\cos\theta}\end{bmatrix}
R3yz
|
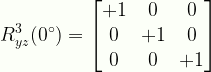
\displaystyle{R}^{3}_{yz}(0^{\circ}) =\begin{bmatrix}{+1}&{0}&{0}\\{0}&{+1}&{0}\\{0}&{0}&{+1}\end{bmatrix}
R3yz0
|
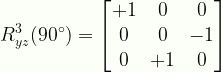
\displaystyle{R}^{3}_{yz}(90^{\circ}) =\begin{bmatrix}{+1}&{0}&{0}\\{0}&{0}&{-1}\\{0}&{+1}&{0}\end{bmatrix}
R3yz90
|
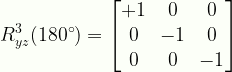
\displaystyle{R}^{3}_{yz}(180^{\circ})=\begin{bmatrix}{+1}&{0}&{0}\\{0}&{-1}&{0}\\{0}&{0}&{-1}\end{bmatrix}
R3yz180
|
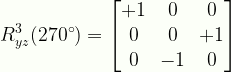
\displaystyle{R}^{3}_{yz}(270^{\circ})=\begin{bmatrix}{+1}&{0}&{0}\\{0}&{0}&{+1}\\{0}&{-1}&{0}\end{bmatrix}
R3yz270
|
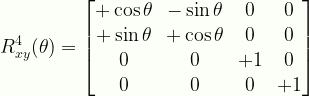
\displaystyle{R}^{4}_{xy}(\theta)=\begin{bmatrix}{+\cos\theta}&{-\sin\theta}&{0}&{0}\\{+\sin\theta}&{+\cos\theta}&{0}&{0}\\{0}&{0}&{+1}&{0}\\{0}&{0}&{0}&{+1}\end{bmatrix}
R4xy
|

\displaystyle{R}^{4}_{xz}(\theta)=\begin{bmatrix}{+\cos\theta}&{0}&{-\sin\theta}&{0}\\{0}&{+1}&{0}&{0}\\{+\sin\theta}&{0}&{+\cos\theta}&{0}\\{0}&{0}&{0}&{+1}\end{bmatrix}
R4xz
|
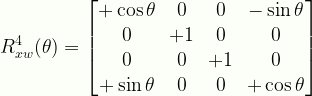
\displaystyle{R}^{4}_{xw}(\theta)=\begin{bmatrix}{+\cos\theta}&{0}&{0}&{-\sin\theta}\\{0}&{+1}&{0}&{0}\\{0}&{0}&{+1}&{0}\\{+\sin\theta}&{0}&{0}&{+\cos\theta}\end{bmatrix}
R4xw
|

\displaystyle{R}^{4}_{yz}(\theta)=\begin{bmatrix}{+1}&{0}&{0}&{0}\\{0}&{+\cos\theta}&{-\sin\theta}&{0}\\{0}&{+\sin\theta}&{+\cos\theta}&{0}\\{0}&{0}&{0}&{+1}\end{bmatrix}
R4yz
|
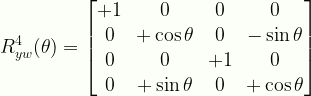
\displaystyle{R}^{4}_{yw}(\theta)=\begin{bmatrix}{+1}&{0}&{0}&{0}\\{0}&{+\cos\theta}&{0}&{-\sin\theta}\\{0}&{0}&{+1}&{0}\\{0}&{+\sin\theta}&{0}&{+\cos\theta}\end{bmatrix}
R4yw
|

\displaystyle{R}^{4}_{zw}(\theta)=\begin{bmatrix}{+1}&{0}&{0}&{0}\\{0}&{+1}&{0}&{0}\\{0}&{0}&{+\cos\theta}&{-\sin\theta}\\{0}&{0}&{+\sin\theta}&{+\cos\theta}\end{bmatrix}
R4zw
|
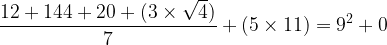
\displaystyle\frac{{12}+{144}+{20}+({3}\times\sqrt{4})}{7}+({5}\times{11})={9}^{2}+{0}
limerick1
|
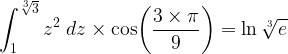
\displaystyle\int_{1}^{\sqrt[3]{3}}{z}^{2}\;{dz}\times\cos\!\left(\frac{{3}\times\pi}{9}\right)=\ln\sqrt[3]{e}
limerick2
|