Sonnack.com

A time and a place…

Last time I introduced you to the idea of a space-time event. In physics, an "event" has the same meaning as when Hollywood blares out about a "major motion picture event" — that is to say, nothing at all special — just something that happens at a specified location and time.

If you attend a social event, it has a location and a time. When we talk about space-time events, all we mean is a specific location and a specific time (hence the name, space-time event).

Today we'll explore some interesting aspects of such events.

I want to emphasize that a space-time event does not require that anything special happen. Any specified location in space, along with a specified time, comprises an "event." (Of course, we usually are interested in events where something interesting does happen. That's why we're interested.)

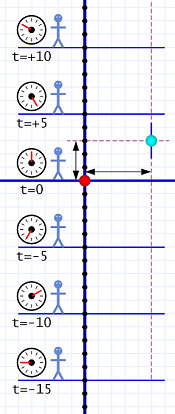Diagram 1. Al sees an Event.

We'll start with a time-space diagram that shows Al just hanging out. He's not moving, so his world line is strictly vertical. (Remember that Al's location is the line, not the stick figures — those are just decorations!) We'll consider his location as the physical origin (x=0).

He has a timer that, like a rocket launch, starts with a "T minus" countdown, reaches zero (t=0), and then continues in a "T plus" fashion. I've included a series of snapshots taken every five ticks.

Calling his location x=0 is arbitrary, and so is the t=0 mark. We could just as easily consider his location x=42 and have started the timer many hours ago. Placing the space-time origin conveniently just simplifies any calculations we might make.

The cyan dot on the diagram indicates an event that interests Al.

It has a definite location some distance from Al, and it happens at a definite time. From the diagram we can see that its space coordinate is x=+5 and its time coordinate is t=+3.

The question we address today is how we can know that.

There are actually two questions to answer: How can we know the location of an event? How can we know the time of an event? It's the latter question that turns out to be a little bit tricky.

In our previous hallway examples, the floor tiles gave us a way of measuring distance. Even if we're outside (or inside on a carpet), we can imagine a system of tiles. Al can wander around with a single tile (or a ruler) and mark off units of distance.

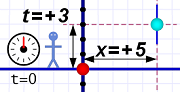Diagram 2. With close events we can just look at the timer.

Once we do that (even if we just imagine it), we can assign spacial coordinates. If we designate any given point as zero (the origin), all other points are some distance (plus or minus) from the origin.

So Al is able to see that the event in question happened five tiles (or grid marks) away.

The tougher question is: When did it happen? How does Al know, for sure, that it happened at t=+3?

If it's close enough, Al can just look at his timer and note the reading. He is justified in saying that nearby events happen simultaneously.

But we know that even light takes some time to travel, so the further away an event is, the longer it takes for us to see it. Remember that the Moon's light takes about 1.3 seconds to reach our eyes, and the Sun's light takes over 8 minutes!

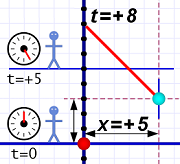Diagram 3. With distant events, it takes some time for the light to reach our eyes.

Since the speed of light is always constant, if we do know the distance, we can calculate the travel time. Then we can take the time the event's light reaches us and subtract that travel time to give us the time the event actually happened.

In diagram 3 we're imagining the event is far enough away that it requires five ticks of the timer for the light (the red line) to reach us (we can call this distance: 5 light-ticks). If Al knows this, he can subtract the light's travel time from when he sees it (at t=+8) and get the correct answer (t=+3).

Of course, if we don't know the distance, the trick doesn't work. Let's say we want to know about an event on a passing asteroid (that is: where it is at a given moment). In this case we don't know its distance.

But light can still help us measure both the distance and the time.

If we shine a laser at the asteroid, we can measure the time the light takes to get there and back (that is: when we see the reflected light). We subtract the start time from the end time to get the round-trip time and divide that by two. This gives us the time light took to go one way.

Since light always travels at the same speed, we can use that one-way time to calculate the distance (this is just the reverse of using a known distance to calculate light's travel time).

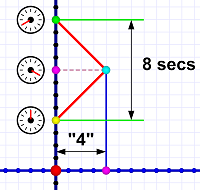Diagram 4. Bouncing light (red lines) off an object to measure its distance and time coordinates.

The time of the event — when light actually strikes the object — is halfway between the start and end time.

All of this raises some important points that will take another post to clarify. I'm going to leave that for tomorrow, because a full understanding of this stuff here is the foundation of what's coming next week.

In the meantime, a couple of observations:

The light from nearby events does take time to reach our eyes, but we can usually ignore it. It takes light about one nanosecond to travel one foot (or for metric folks: about three nanoseconds to travel one meter).

A nanosecond is 0.000000001 second (one-billionth of a second), so the light from events within a room, train car, or back yard, reach our eyes pretty much instantly.

It only takes light 0.000001 second (one-millionth of a second) to travel more than three football fields (1000 feet), so even sports venues show us events whose light reaches us — for all intents and purposes — instantly.

It's only when we deal with extremely long distances (like Earth to the Moon) that the delay in travel time becomes significant.

You may have noticed that the light beams in diagram 3 and diagram 4 move at a 45-degree angle. Astute or experienced readers will recognize that this implies either great distances or extremely short timer ticks.

Indeed it does, and that will be tomorrow's topic.

Even if we were able to see Mount Everest all the way from Mumbai, India (which is about 1000 miles away), it still takes only a bit more than 5 milliseconds (0.005 seconds) for its light to reach your eyes! Light is fast!