SR #7: Dueling Diagrams
 Rashomon!
Rashomon!The last two posts introduced and explored the concept of time-space diagrams. This time I'll complete that exploration by using them to consider motion from two points of view. This will be an exercise in application of our diagrams.
I'm going to connect that application with something I stressed last week: that motion has a symmetrical component. It's perfectly valid to think of the world moving past the train as it is to think of the train moving through the world.
It happens that here our dueling points of view are resolved by something else I discussed last week. See if you spot it before I mention it.
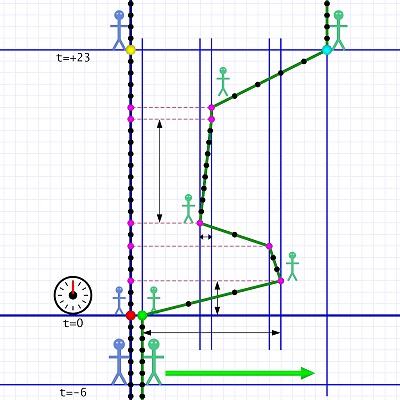
Today's scenario involves just our friends Al and Em back in that narrow hallway. They start off standing next to each other, and — after some back and forth motion — they end up much further apart.
In the first version, Al stands still while Em moves back and forth, closer and further from Al. When she's done, she ends up at some distance from Al, and she stands still at that point.
Remember: these diagrams show space in only one dimension — left and right. Up and down is the time dimension (up is forwards in time). Em is not walking up the diagram, she is only walking back and forth.
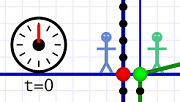 Red dot marks t=0 & x=0.
Red dot marks t=0 & x=0.As we did yesterday, we'll think of the grid work as floor tiles. We're going to call Al's position the origin; tile zero. (The red dot usually indicates the time-space origin.)
At first, Em stands next to Al. The diagram shows that they've been standing together for at least six or seven ticks of the timer.
Our time zero (t=0) is the moment Em begins moving, so their prior time has negative time coordinates. The bottom of the diagram has a snapshot taken at -6 ticks. (Think of a rocket launch: "T minus six and counting." Same thing.)
At the top we have another snapshot, this one taken at +23 ticks when Em stops moving.
Each person's time-space line (or world line) has dots that represent the ticks of the timer shown on the left. Al stands motionless on the zero tile, so his world line is strictly vertical.
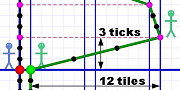 12 ÷ 3 = 4 tiles per tick
12 ÷ 3 = 4 tiles per tickEm starts by moving away from Al very rapidly. She moves 12 tiles in just 3 ticks. She takes another 3 ticks to move back towards Al just 1 tile. Notice the difference in the spacing of her tick dots. The further apart those dots are, the faster Em is moving.
(Al's "time tick" dots are the most closely spaced because he's not moving at all.)
Next Em moves closer fairly rapidly (6 tiles in 2 clicks), but then very slowly backs away just one tile (taking 9 ticks to do it — notice how closely space the tick dots are). She stands still for 1 tick and then moves to her final position 16 tiles away (covering 10 tiles in 5 ticks).
Each time Em changes direction a horizontal dashed line measures her distance from Al. Purple dots mark these points for both Em and Al, and those purple dots represent events of interest.
An event is a point in space and time. An event has both a spacial coordinate and a time coordinate.
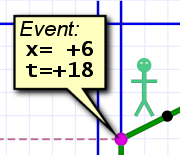 A space-time event!
A space-time event!In our simple one-dimensional diagrams, a spacial coordinate is a single number: the number of tiles between the event and the origin. We call this the x coordinate.
Al stands on the origin, which we define as x=0. Since Al never moves, his x coordinate never changes (of course his time coordinate, t, does).
When she's moving, Em has a changing x coordinate. She starts off at +1 (one tile to the right of Al), moves to +12, back to +11, then all the way back to +5. Next she slowly moves away to +6, stands there for one tick, and lastly moves to her final position, x=+16.
Al and Em have (shared) time coordinates. There is only one dimension of time, so again there is a single number to deal with.
At the origin, by definition, they both have t=0 and Em launches into her journey. At +3 Em changes direction. She speeds up at +6 and changes direction again at +8. She stops briefly, from +17 to +18 before moving to her final position at t=+23.
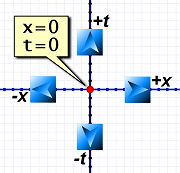 space-time coordinate system
space-time coordinate systemNote that Al's time coordinates match Em's, although his spacial coordinates do not. The speeds involved here are slow enough that Al's and Em's clocks agree.
If they each carried a timer, which they synchronized at t=0, their timers would agree when they met again.
Recall that a key aspect of relativity is the symmetry of points of view. Different frames of reference can each claim they are not moving while the other is (or vice versa).
Therefore Em seems justified in claiming that Al (and the hallway!) are moving while she stands still.
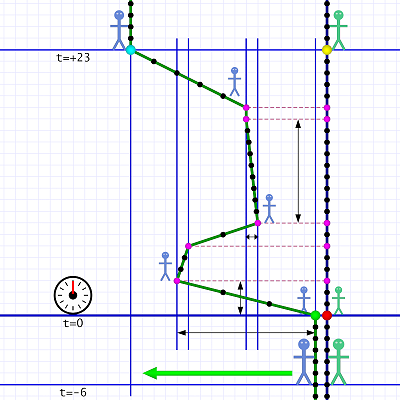
Here's a diagram showing that point of view:
If you compare this with diagram 1, you can see they are basically mirror images of each other, but this time we're defining Em's position as x=0.
Again, Al and Em start off standing 1 tile apart, and again they end up standing 16 tiles apart. Since we're considering tiles to Em's left, and since we're also calling Em's position the origin (x=0), Al's spacial coordinates have minus signs.
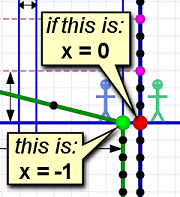 Left means minus x!
Left means minus x!That is, Al starts on tile -1 and ends up on tile -16. This actually makes no difference to our calculations because they depend more on the difference in distance, not whatever specific numbers we happen to use.
Our system of time coordinates remains the same. Movement begins at t=0 and ends at t=+23.
As far as the distance and time (and therefore speed) calculations go, the situations are symmetrical. Either diagram works for these calculations.
But Em is not justified in claiming she's motionless and Al is really the moving one. Have you figured out why?
It's not because it requires the hallway to move along with Al. As we've seen before, you are fully justified in claiming a train you're on isn't moving, but the whole world is moving past.
 This changes the story!
This changes the story!It's because Em changed directions! (Several times.) At the instant Em changes direction (or starts moving or stops moving), her speed changes. She experiences acceleration!
Al does not because he really is standing still in the hallway (and Em really is the one who is moving). Al does not change directions.
The key is in the purple event dots. Al experiences no change at his purple points — which we would expect given diagram 1.
But Em does! The way diagram 2 depicts her world line is incorrect. She cannot be standing still.
Because this series is about Special Relativity — which requires constant motion — this is likely the only time I'll diagram changing motion. The main reason for doing it this time was to introduce you to the idea of space-time events.
That's what I'll be discussing in detail next time!
 …of a SpaceTime nature!
…of a SpaceTime nature!