SR #10: Simultaneous Events
I wish my laser had tick marks!In the last two weeks I've covered relative motion as the ancients understood it (Galilean Relativity), touched on how light doesn't follow those rules, and introduced time-space diagrams that we can use to visualize motion. I also introduced the topic of space-time events, which are simply locations in space at a given time.
In particular, I showed how our friend Al can use a laser to determine both the location and the time (relative to himself) of an event. This allows him to map his nearby space and time using a system of regular (that is, grid-like) space-time coordinates.
Today we continue with that idea.
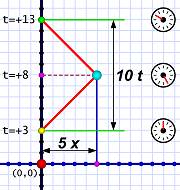Diagram 1. Event @ (5x,8t)The main idea here is that Al can shine his laser at a distant object and time how long it takes for him to see the light hit that object.[1] Divide the round-trip time by two to get the one-way time.
Since light always travels at the same speed, it makes a very good ruler. (And, as we'll see later, also a good clock.) The one-way travel time tells Al how far away the object is.[2] In this case (diagram 1), 10 timer ticks means the event is 5 light-ticks away.
He can also use the send and receive times to determine when the event (of light hitting the object) occurred. That's a point halfway between the two times. In diagram 1, Al sends a light pulse at t=+3. Adding the 5-tick one-way travel time tells him the event happened at t=+8.
Al can also work backwards from the time he receives the reflection (at t=+13). Subtracting the (one-way) travel time gives the same answer, t=+8.
Backwards is especially useful when the event's distance is known and the event produces its own light (i.e. is visible)! Then Al doesn't have to send his own light. He knows the light reaching him from the event took a time given by the distance divided by light's velocity.
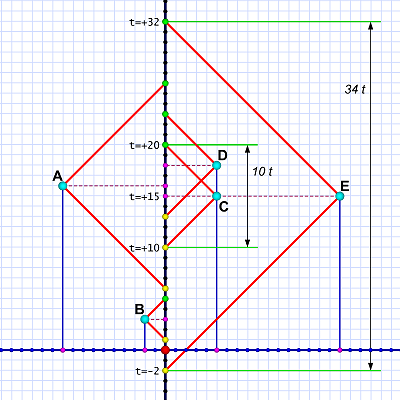Diagram 2. Lots of Events to map!Diagram 2 shows five events (cyan dots, A–E) scattered at various distances and times relative to Al (who is represented by the thick vertical line). The large red dot marks t=0 and x=0.
Thin blue lines project the events to their distance coordinate on Al's x axis; dashed lines project their time coordinate onto his t axis. In both cases, there are purple markers at those coordinates.
The red lines are laser beams sent by Al and reflected off the events. Yellow markers indicate their start time; green markers return time. Green lines and black arrows call out the light travel time-spans to and from events B, C, and E.
Hopefully by now you can easily see how Al determines that event B is two light-ticks away (x=-2 — minus because it's to Al's left) and occurred at t=+3. Therefore event B has a space-time coordinate of -2x, +3t.[3]
Likewise, event C, has a space-time coordinate of +5x, +15t, and the more distant vent E is located at +17x, +15t.[4]
The interesting thing here is that both event C and event E have the same time coordinate, t=+15. This means, according to Al, they all happen at the same time — they are simultaneous.
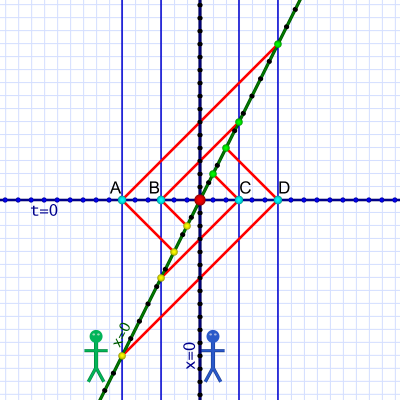
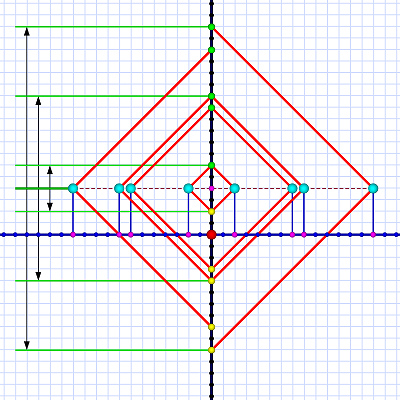Diagram 3. Lots of simultaneous events!In diagram 3 we have a set of eight events that Al sees as simultaneous. From his perspective, all eight happen at t=+4. They happen at various distances, no two x coordinates are the same, so they are scattered in space, but identical in time.
While the laser bounces start and end at various times, they all center on the +4t coordinate. The diagram has a rough diamond symmetry based on this center line.
A critical point here today is how simultaneous events line up in a horizontal line (and why).
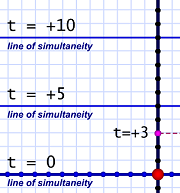In sync, on five!This means that horizontal lines on our diagrams represent lines of simultaneity.
Everything at rest relative to you experiences the same timer ticks and therefore agrees on what events happen simultaneously. If you call a friend on the phone you can both watch the same TV show simultaneously because you're both at rest (more or less) relative to each other.
Al and Em can stand next to each other and synchronize their watches. Em can leave and observe an event from close by. Al watches the same event from a distance. When Al and Em meet again, they can compare when they saw the event, thus confirming Al's tests with light beams.
Given that any location and moment can be an event, this process justifies Al's regular coordinate system of relative distances and timer ticks. His sense of where things are in space and time admits to a regular grid of timer ticks and spacial "tiles."
The question now is: What happens if Em comes flying past Al at very high speed? Does she see the same thing Al sees? That's where I'll pick up tomorrow.
Tomorrow! Em comes flying past Al at 1/2 c![1] You may never have really thought about it, but when you shine a flashlight (or a laser cat teaser) at something, the light goes from the device in your hand, hits the object, and then (some part of that light) is reflected back to your eye. Light has to go there and back again for you to see anything.
[2] This is also how radar works, except radar uses radio waves — which are a type of light and which therefore travel at light speed. They're just not a type of light we can see. A radar set sends out a blast of radar "light" and then times how long it takes to see the reflection.
[3] The light beam for event B starts at +1t and ends at +5t; the total travel time is 4 ticks — 2 ticks one-way.
Event B is therefore located -2x light-ticks away. Al saw its light at +5t; subtract the travel time; the event occurs at +3t.
[4] Event C: light path starts at +10t and ends at +20t; the total travel time is 10 ticks — 5 ticks one-way. Subtract 5 from 20 to get an event time of +15t. Distance is obviously +10x light-ticks.
Event E: light path starts at -2t and ends at +32t; the total travel time is 34 ticks — 17 ticks one-way. Subtract 17 from 32 to get an event time of +15t. (Distance is +17x light-ticks.)