SR #11: Simultaneous, Not!
 Magic tick marks again!
Magic tick marks again!Last time our friend Al used lasers and timers to create a regular grid-like map of the space and time near him. The map allowed him to assign space-time coordinates to events in his frame of reference (even if it takes time for him to see light from those events).
An important concept is the idea of simultaneity — of events in different locations happening at the same moment according to some observer (who has to wait for the event's light to reach their eye).
So far the events weren't moving relative to us. What if we — or the events, same thing — are moving (and moving fast)? It turns out, this changes the picture!
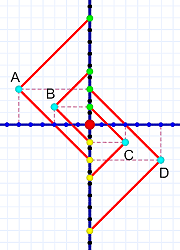
We'll start where we left off last time. Al stands motionless in the center (but moving upwards in time). His vertical world line defines x=0. There are four events (cyan dots) that interest Al: two to the left, A and B, and two, C and D, to the right. Their vertical lines show that none of them move relative to Al.
As before, Al bounces laser beams (red lines) off the events to determine their position and time. Red lines indicate laser light moving through space-time (a yellow dot marks the start; a green dot marks the end).
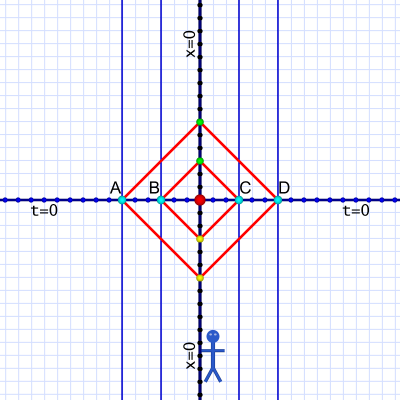 Diagram 1a. Al's view of events A, B, C, & D.
Diagram 1a. Al's view of events A, B, C, & D.According to Al, all four events occur simultaneously. His observations place all four on the same horizontal line — the same moment in time as Al clocks it. We'll think of that event moment as t=0.
If Al knows the exact distance of the events, he knows how long it takes their light to reach him. He can just subtract that time from the arrival time. (When we only consider light from the event, we ignore the lower half of the diagram's pattern.)
 Symmetry of Synchronicity
Symmetry of SynchronicityThere's an obvious symmetry to these diagrams. It's enhanced in this case because the events are equally spaced, but even yesterday's diagram — pictured to the right — displays that symmetry despite eight scattered (but simultaneous) events.
The symmetry comes from how the time spans will vary in total length (depending on the distance to the events), but they all center on the same time instant — the horizontal line of simultaneity.
Important: Al doesn't see all four events at the same time — or even right when they happen. The light from all four takes time to reach him. Events B and C are closest, so Al sees their light first. (They're the same distance from Al, so he sees their light simultaneously.) Events A and D are further, so Al sees their light later (and again simultaneously due to their matching distances).
A rendering of the set up in semi-3D-ish might look something like this:
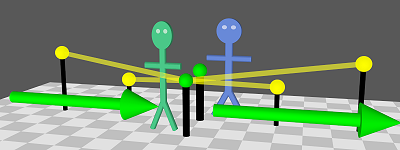
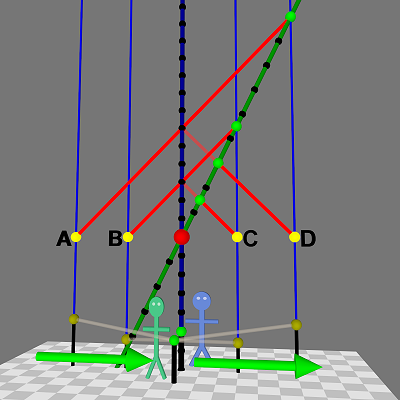
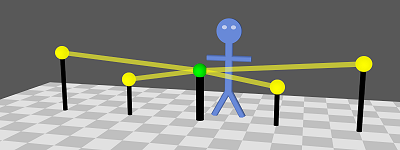 Al, with his light detector, and four event marker thingies.
Al, with his light detector, and four event marker thingies.Al stands in the center next to his light detector (green sphere). On either side of him are the four event marker thingies (yellow spheres). Al's light detector receives light flashes (yellow beams) generated by the marker thingies.
To simplify the picture, we're assuming a known distance to the events (using the floor tiles) and timing the light only from the markers to the detector (rather than both ways). Al knows when they flash by subtracting the flash travel time from the detection time.
If we combine the time-space diagram of the event flashes traveling to Al's detector with our semi-3D-ish picture we get something like this:
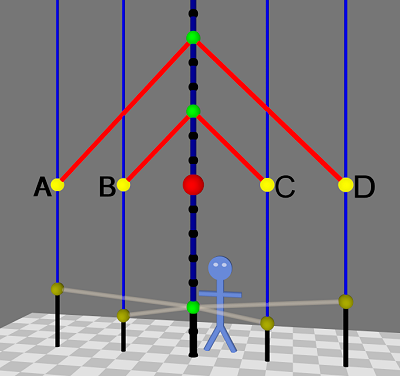 Al's detector sees light from simultaneous event flashes.
Al's detector sees light from simultaneous event flashes.The vertical blue lines show how Al (his light detector, technically) and the event markers don't move in space (but do move upwards in time).
The red sphere marks the (0x, 0t) space-time origin point, the moment the event markers flash. Note that their light doesn't reach Al's detector in the center for several ticks. First light from B and C reaches him, then the light from A and D gets to him.
Now let's imagine that Em comes speeding past:
 Here comes Em! Hi, Em! There goes Em!
Here comes Em! Hi, Em! There goes Em!She's moving very fast — half the speed of light (or: c/2).
That's over 300 million MPH (over 500 million KPH)! It's only at these high speeds that the effects of Special Relativity become pronounced. (The gamma factor at c/2 is still only 1.1547 — still pretty close to 1.0000. In other words, SR effects are pronounced at c/2, but not huge; about a 15% effect when going half the speed of light.)
As she passes, Em's going to repeat Al's experiment of shining lasers at the event markers and measuring the time it takes to see the reflection. Here's the diagram showing what Al sees her do as he stands there watching her pass by:
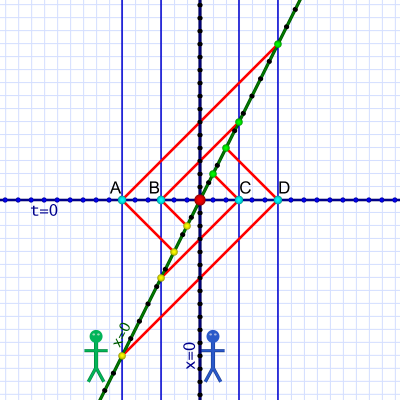 Diagram 2. Al watches Em come speeding past at c/2.
Diagram 2. Al watches Em come speeding past at c/2.The thick green line is Em's motion through Al's frame of reference as Al sees it. She starts off on the left, comes closer, passes him, and keeps going off to the right.
At the moment Em passes Al (at the red dot), they're going to "high five" and synchronize their timers to "T-Zero." Remember this is the moment Al calls (0x, 0t) and considers simultaneous with all four events. Em and Al can agree on that point only because they're both at that point at that moment.
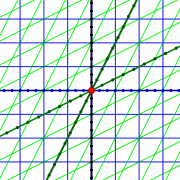 Different coordinate systems!
Different coordinate systems!(As it turns out, that is the only point where their coordinate systems match! Their timers run at different rates, so their time coordinates don't match. In fact, neither do their space coordinates! But they can agree to "pin" the two systems at some mutual point.)
Important: Even though Em is moving, the laser light she uses still travels at c — always at a 45-degree angle on our diagrams. The combination of that and her movement result in a very different diagram than for Al (diagram 1).
Because she's moving at a constant rate, Em claims she is standing still while everything else is zipping past. Physics has to work normally in her frame of reference, so she can map her space-time the same way Al does.
In her coordinate system, Em draws a different diagram — one that shows her standing still while Al and the events pass by:
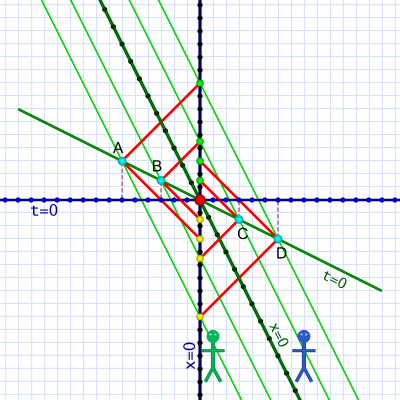 Diagram 3. Em's frame of reference as Al and events pass her.
Diagram 3. Em's frame of reference as Al and events pass her.Em considers herself standing still and identifies her position as x=0 (and measures distances relative to herself). From her perspective, Al and the events pass by from right to left.
In her frame of reference, Em has her own horizontal lines of simultaneity. She agrees with Al to use the red dot as an origin point. That gives her a t=0 line. Now she has a coordinate system.
The green dotted line shows Al's world line through Em's frame of reference (just as diagram 2 showed Em's path through Al's). The event marker locations — which are moving relative to Em, but motionless relative to Al — have world lines parallel to Al.
 Simultaneous, Not!
Simultaneous, Not!Diagram 3 shows Ems perspective of shining her lasers. Light always travels at 45 degrees in these diagrams, so the path is determined by the start and end times. Given those times, the light has to follow a certain path.
Em sees the four events at different coordinates in her space-time. In particular, since they don't lie on a horizontal line — the events are not simultaneous to Em!
Specifically, as she sees it, D happens first and C happens later. Then she crosses the origin and high-fives Al as she passes him. After than comes B and finally A comes last. They may happen in quick succession — Em sees them spread out over only six timer ticks — but they're definitely not simultaneous.
Of course, Em knows the events are moving, and she can use this information to recognize that Al sees them as simultaneous even if she doesn't. The point is that she doesn't. Em sees events in a different order than Al does!
We'll pick up with this next time!
 Al watches Em zip by at c/2.
Al watches Em zip by at c/2.