Sonnack.com

Peace Train!

Last time we explored the Simultaneous Lightning Strikes illustration of Special Relativity. In that scenario, on-the-ground observer Al sees simultaneous lightning strikes to a passing (very) high-speed train. On-the-train observer Em agrees both bolts hit the train (one front; one rear), but sees one happening first followed by the other.

The next scenario reverses the situation. This time traveler Em sees simultaneous events on the train and bystander Al sees them happening one after the other.

Today we explore: Peace Treaty (on a Train)!

The usual story for this visualization is that two nations are about to sign a peace treaty. Relations are highly strained, so they've set up a bizarre protocol where an electronic document signing machine sits on the center of a table and flashes a light when it's time to officially ratify the treaty.

The two enemy ambassadors sit at opposite ends of a long table. Each has a device with a button and a light. When they see the treaty machine flash, they both signify agreement by pressing their buttons — which causes their lights to light up.

If the treaty machine sees both their lights go on simultaneously, it goes ahead and ratifies the treaty (otherwise it shuts down and sulks; possibly it explodes).

By the way, did I mention they're on a train? They're on a train.

This is all a cute way of setting up a situation where a light flashes at the midpoint of the train. The light flashes travel up and down the length of the train, bounce off mirrors placed at both ends of the train, and returns to the center where it's detected.

It's the simultaneity test in disguise — bouncing light off two locations to see if the events of the two bounces are simultaneous. Here the ambassadors and their button-lights play the role of light bouncing off a distant object. The treaty machine is the light "radar."

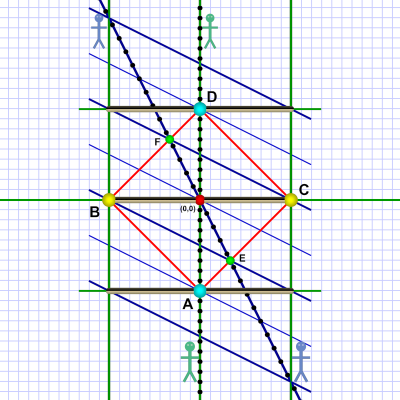
So this should really almost be old hat for you by now. Here's the situation from Em's frame of reference (on the train):

Diagram 1. Em sees simultaneous events B & C. Al passes by.

The vertical dotted line up the center is Em's world line (the dots represent her timer ticks). She's at the midpoint of the train. The green vertical lines on either side represent (right) the front of the train and (left) the rear of the train.

Event A, at t=-9t, is the machine (also at the train's midpoint) giving off a flash. The light travels up and down the train (right and left). At each end it bounces off mirrors (events B & C, at t=0) and returns to the center at event D, at t=+9t.^[1]

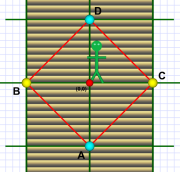Train sweeps!

The diagram shows three snapshots of the train at +9t, 0t, & -9t. (Remember the train is actually sweeping from bottom to top as covers all points along that sweep. It's only shown at those three moments.)

Meanwhile, Al passes by — his world line (with timer-tick dots) runs from right to left (bottom to top).

It doesn't actually matter whether Al speeds by in a relativistic sports car while Em's train just sits motionless relative to the track, or if Al stands motionless by the track and Em's train speeds by. It literally makes no difference here.

As usual, both consider the point where they pass (red dot) as the origin. Some of Al's lines of simultaneity are shown as short lines in blue.

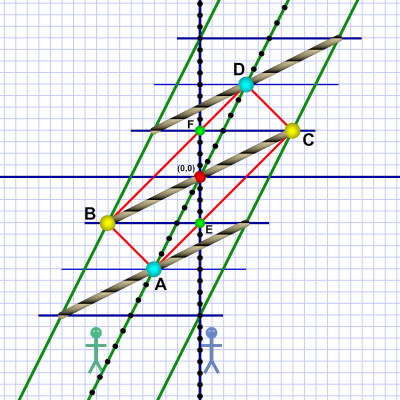
Here's the same picture from Al's perspective:

Diagram 2. Al's view of events B & C as Em passes by.

Just like yesterday, from Al's perspective Em's coordinate system, and the train that's part of it, is rotated out of his horizontal lines of simultaneity.

Al and Em have to agree about the order of events on the train: The machine's light flash from the center travels to both ends, bounces off mirrors and returns to the center.^[2] But they may disagree about the timing (the simultaneity) of those events.

Due to the significant difference in their relative velocities, the picture they see of the other coordinate system is rotated. Their own coordinate system always looks perfectly normal (that is: regular and rectangular).

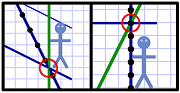Al passes front of train.

Yet note how Al's lines of simultaneity still intersect the same events.

Both diagrams show him passing the front of the train at the same moment (the lowest line of simultaneity). Both likewise show him passing the rear of the train at the same moment (the highest line).

One interesting aspect of diagram 2 is how both light paths have a longer and shorter leg. The two paths are mirror versions of each other, so the total trip time is the same for both. Since Al and Em always agree on what events happened (just not when), both must see the light paths begin and end together (events B & C).

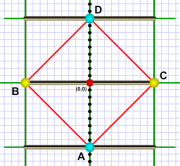Em's diamond symmetry

For both paths to begin and end in synch requires some type of symmetry to the paths. In diagram 1 (Em's perspective), there is a diamond pattern, the sign of simultaneous events (and equal distances).

This is a crucial point: From Em's perspective, all path legs are the same length; there are no longer or shorter legs!

Em sees things inside the train the same as she would them inside a room of a house.

From her perspective, light goes forwards and backwards exactly the same way. Thus, a diagram showing her frame of reference displays a diamond pattern with equal-length legs.

On the other hand, Al sees light moving towards the front of the train traveling longer in order to catch the train moving away from it. He also sees light moving towards the back of the train taking a shorter path due to meeting the oncoming train.

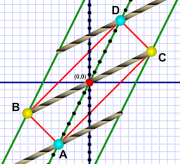Al's rhomboid symmetry

In diagram 2, which shows things from Al's perspective, the light path has a rhomboid shape. The path still has a symmetry — but the corners of the path occur at different times.

Em and Al must agree light bounces off the mirrors^[3], but since those events are separated in space, Al and Em don't have to agree on the timing of those events. They only have to agree on things that happen at a given point. (For example, the moment they pass each other. Both agree they're at that location at that time. They can use this to agree on a mutual origin point).

Keep in mind that all this is true on any train (or bus or plane), but the effects are buried behind more than 15 decimal point zeros. Several more if we're talking bus. In terms of time, the difference amounts to 500 zepto-seconds at 55 MPH.^[4] (You reach 40 atto-seconds at 500 MPH!)

And that's about it for the second train example. It's the first example turned around. Both illustrate how simultaneity is relative under Special Relativity. The final example, the Too Long Train, illustrates another property of SR: length contraction!

See you at the train station!

^[1] Or, if you prefer the original version: The machine's light flash travels up and down the train. The two ambassadors see the flash simultaneously, and both press their buttons to flash their lights simultaneously. The ambassadors' light flashes travel back to the center where the machine detects them.

^[2] Or, the machine flashes, light travels to the ambassadors, who see it and press their buttons. Their light flashes travel back to the center where the machine detects them.

^[3] Or, you know, ambassadors pushing buttons.

^[4] It goes: milli, micro, nano, pico, femto, atto, zepto, yocto.