Sonnack.com

And the winner is…

In the last two posts I've explained how Special Relativity is about relative motion between two frames of reference, and that the motion involved is constant, straight line motion that allows us to view either frame as the "moving" one or the "standing still" one.

Today I'm going to dig a little bit deeper into the idea of relative motion and what that involves for actions within a constantly moving frame of reference versus what observers in a different frame perceive. In other words: trains, planes, and automobiles.

(Warning: this gets a little math-y, but you can ignore those bits.)

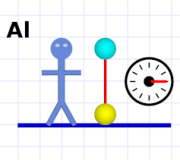Diagram 1 (watch your toes!)

Let's say you're holding up a bowling ball and you drop it.^[1] Exactly as you expect, it falls straight down and hits the floor. (Watch out for your toes!)

It falls very fast, but it does take some amount of time to fall. If we had quick reflexes and a good stopwatch, we could measure the amount of time.

In diagram 1 we see that our friend Al has performed this experiment. The cyan-colored ball shows the starting position, the yellow-colored ball shows the final position. To the right is a stop watch that has measured three ticks (let's call them milli-jiffies) for the ball to fall.

Now let's imagine that our friend Em performs the same experiment. A key tenet of physics is that identical experiments performed in different frames of reference always have identical results.^[2]

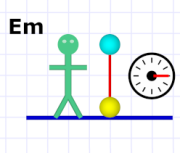Diagram 2. Three ticks for Em.

That means that Em gets the same three milli-jiffy result as she times the falling bowling ball (we assume she drops it from the same height — if she didn't, she would get a different time).

What I didn't tell you is that Em is actually on a moving train traveling past Al (but remember, from her point of view, she is still, and Al is traveling past her). As you can imagine, since Em perceives herself as standing still (just as Al does), she must get the same result as Al does.

If Al watches Em as she passes, he sees that her stopwatch and his agree. They see that both experiments take three ticks. But consider what Al actually sees as Em passes. We'll assume Em is moving from Al's left to his right.

If Em is moving (according to Al), so is the falling ball (and the stopwatch and everything else in Em's frame of reference). However the ball is not only moving left to right, it's also moving down! From Al's point of view, it looks like this:

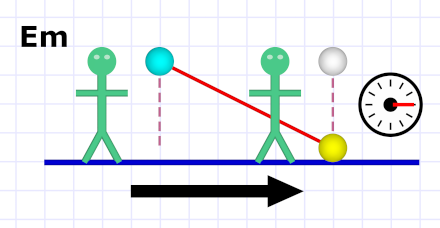Diagram 3. What Al sees when Em drops the ball.

According to Al, Em's falling ball moves in a diagonal path!^[3] He also sees Em's stopwatch and knows the ball took three ticks to move along the diagonal path.

If Al and Em both drop their bowling balls from a height of three cubits, they both calculate the ball's fall rate (its speed) as one cubit per milli-jiffy (simply: 3 cubits ÷ 3 milli-jiffies = 1).

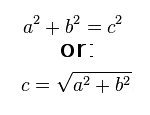Pythagorean theorem

But as you see in diagram 3, Al also sees that Em's ball moves six cubits to the right as it falls. He can use the Pythagorean theorem to calculate the total distance it moves: a smidgen over 6.7 cubits.^[4]

If Al divides this by the three ticks it takes to fall, he sees that Em's ball is moving over twice as fast (a hair under 2.24 times) as his.^[5]

Now consider what the situation looks like from Em's point of view as she — considering herself as standing still — watches Al pass her (from right to left from her perspective):

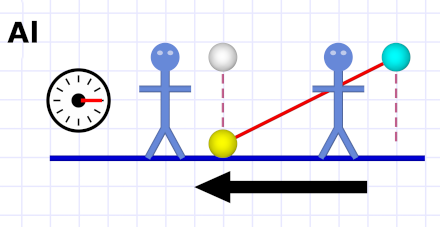Diagram 4. What Em sees when Al drops the ball.

She sees the same picture of Al that Al saw of her (just with the direction reversed). She would make the same calculations of Al's experiment that Al made of hers. And they'd both be right.

This is the critical point: Al sees Em's ball as moving faster (because he thinks Em is moving), and Em sees Al's ball as moving faster (because she thinks Al is moving). And both are correct!

This is the basic form of relativity known to the ancients (who observed that if you drop a rock while passing by the shore on a fast ship, the same sort of situation obtains as with Al and Em).

This idea extends to our infrequent guest, Max, who happens to be performing the bowling ball experiment on a passing plane:

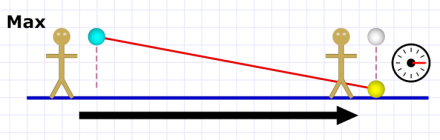Diagram 5. Special guest Max and his (rather slow) plane.

Al sees Max's bowling ball move much faster than Em's did (because Max is moving much faster).

Em, because she's also moving (we'll assume both Em and Max are traveling in the same direction) won't see Max's speed as quite as fast as Al does — her speed deducts from Max's. Yet Max is still moving relative to her, so she sees Max's ball as moving faster (just not as fast as Al does).

Of course, Max sees his bowling ball fall straight down, exactly as Em and Al see their respective balls falling straight down. He also sees their balls moving faster than his the same way they do his.

And that's enough for today. Next time we'll pick up with the idea of relative motion — how speeds combine — and how there turns out to be a critically important exception!

If you are wondering what happened to the automobiles… how do you think Em and Max got to the train station and the airport in the first place?