SR #3: Relative Velocity
![Mo'ne Davis [Mo'ne Davis]](img/sr3-0.png) Throwing like a girl!
Throwing like a girl!I've introduced the idea of an inertial frame of reference. This is when we, and objects in our frame, are either standing still or moving with constant (straight-line) motion. In this situation, we can't tell if we're really moving or standing still relative to some other frame of reference. In fact, the question is meaningless.
I've also introduced the idea that objects moving within our frame — moving (or standing still) along with us, but also moving from our perspective — move differently from the perspective of other frames. Specifically, the speed appears different.
Now I'll dig deeper into that and introduce a crucial exception.
Let's start with some terminology.
 Speed is also a classic action movie. (Pity about the sequel.)
Speed is also a classic action movie. (Pity about the sequel.)Speed is a (single) numerical quantity that always combines two ideas: distance and time. A given speed is the rate of some amount of distance per some amount of time. The "per" means division, so speed is simply distance ÷ time.
To make things easier, the time is usually expressed as a single unit: per (one) hour, or per (one) second, or per (one) milli-jiffy. The amount of distance (miles, meters, cubits) in that time is the speed. For example, 60 MPH means 60 miles distance in one hour of time (likewise: 96 KPH means 96 kilometers in one hour).
Velocity is speed in a specified direction. As such a velocity properly includes extra numbers defining the direction. (Math fans will tell you that speed is a scalar, velocity is a vector.) Here we'll be more general with direction. Forward, backward, and so forth, is sufficient for our purposes.
We return to Al and Em. As before, Al is on the ground next to a train track, and Em is on the train that passes by (from left to right).
As Em goes past she throws two baseballs, one forward — with train's motion — and one backward — against the train's motion. We're going to consider the difference between what each of them see.
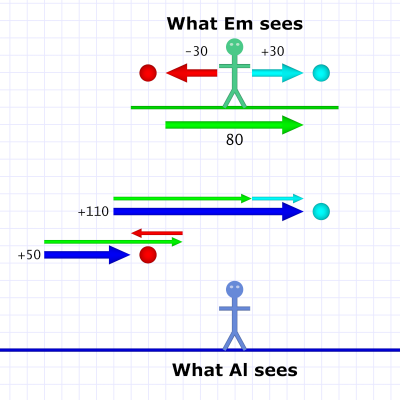 Diagram 1. Em passes Al at 80 and throws balls at 30.
Diagram 1. Em passes Al at 80 and throws balls at 30.In our first example, Em passes Al at 80 MPH (metric readers can imagine KPH throughout). She lobs the baseballs at a fairly slow 30 MPH. She throws the cyan-colored one forward and the red-colored one backward.
From Em's perspective, she sees the both balls moving away from her at 30 MPH. But Al sees Em's whole frame of reference moving at 80 MPH, so this velocity is part of Al's picture!
The forward-moving baseball (cyan) has a velocity in the same direction as the train, so the speeds add together (80 + 30). Al sees that ball moving at 110 MPH.
The backward-moving baseball (red) has a velocity in the opposite direction from the train, so its speed is subtracted from the train's (80 - 30). Al sees that ball moving at 50 MPH.[1]
Since the speed of both balls is less than the train's, Al sees both balls moving "forward" (left-to-right, along with the train). Let's reverse that situation:
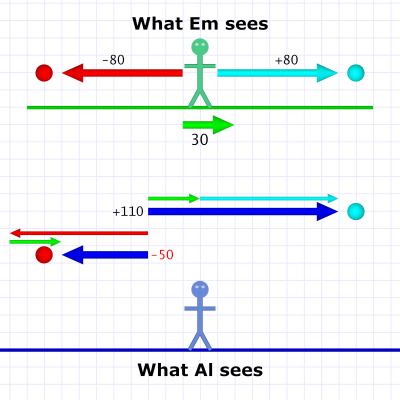 Diagram 2. Em passes at 30 and throws balls at 80.
Diagram 2. Em passes at 30 and throws balls at 80.Now the train is moving much slower than the balls. (Em has a pretty good arm throwing a fastball at 80 MPH — like Mo'ne Davis![2])
The equations are the same, the forward-moving ball's speed adds to the train's, and 30 + 80 is the same as 80 + 30, so Al still sees the cyan-colored ball zipping along at 110 MPH.
Likewise, the backward-moving ball's speed subtracts from the train's (30 - 80)[3], and this gives us a negative answer: -50 MPH. The minus sign just means Al sees that ball as moving backwards at 50.
Of course, Em sees both balls moving at 80 MPH just as she threw them. Now suppose the train and the balls have the same speeds:
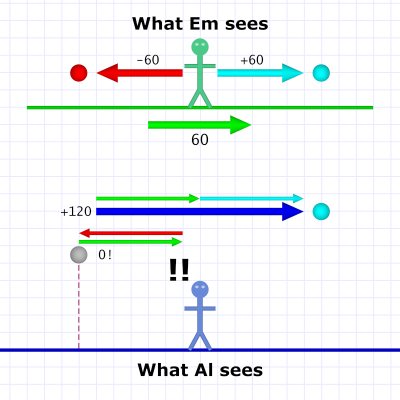 Diagram 3. Em passes at 60 and throws balls at 60.
Diagram 3. Em passes at 60 and throws balls at 60.Both the train and the balls are moving at 60 MPH. As always, Em sees the balls moving away from her at the speed she threw them.
Al still adds the train's speed with the forward-moving ball's speed (60 + 60), so he sees the cyan-colored ball moving at 120 MPH.
He also still subtracts the backward-moving ball's speed from the train's (60 - 60[4]), and this time he gets zero — 0 MPH!
Which means, from Al's perspective, that ball has no speed. If it were free from the train's influence — if it left Em's frame of reference and entered Al's — it would drop straight to the ground.
Mythbusters performed this experiment, and it's worth watching the clip. Just basic physics, but it's pretty cool to see:
https://youtu.be/BLuI118nhzc
We've considered baseballs thrown with velocities that either directly add to, or subtract from, the train's. You might wonder what happens if Em throws a ball in some other direction:
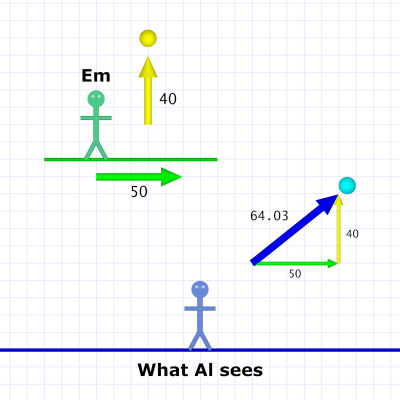 Diagram 4. Em passes at 50 and throws ball at 40 (upwards).
Diagram 4. Em passes at 50 and throws ball at 40 (upwards).Last time we considered balls dropped straight down with gravity providing the speed. Al's calculation of the ball's speed then required Pythagoras and his famous theorem.
Em's thrown baseball here is the same thing. In fact, our additions and subtractions above are reductions of the Pythagorean formula made possible by collapsing one side of the triangle to zero.[5]
Okay, are you ready for the kicker?
This business of adding velocities applies to everything with one very important exception: light. Light always moves at the same speed regardless of your frame of reference! We call that speed: c.
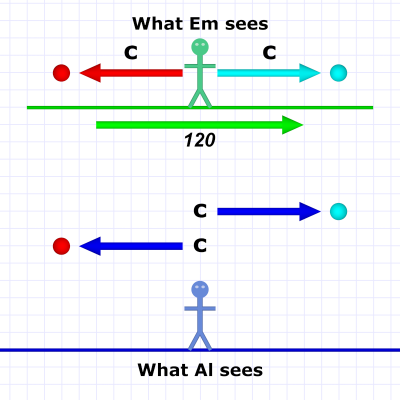 Diagram 5. Em passes at 120 and shines photons at c.
Diagram 5. Em passes at 120 and shines photons at c.The situation described in diagram 5 is different from the first four. In this case Em is shining a light forward and backward as she passes Al (although, remember, she thinks Al is passing her). Em isn't throwing baseballs now — she's throwing photons (cyan- and red-colored ones).
We've given the train a high speed to make the point that it doesn't matter what the speed is. Al sees the photons moving the same speed Em does: at c.
No matter how fast she zips by, both always see light moving at c.
 "You're welcome!"
"You're welcome!"This is the crucial difference between Galilean Relativity (where velocities are added and which the ancients understood) and Special Relativity — which is Einstein's gift.
As we'll see, accepting this fact has some unusual circumstances.
But to fully understand them, I need introduce you to what are called time-space diagrams. They're not that hard to understand, but they are abstract enough to require some explanation.
That will be our primary topic next week. Next time I'll review what I've covered so far, touch a bit more on c, and set the context for Special Relativity.
[1] Technically speaking, the ball's velocity is -30 because we're considering the train's velocity to be +80 (this is part of what we mean by velocity having a direction).
In reality, we're adding in both cases, so the two equations are really (+80)+(+30) and (+80)+(-30) but I wanted to keep things simple.
[2] Slightly better, actually, since Mo'ne tops out around 70 MPH — still about 10 MPH faster than any of her peers (the boys included). There is some chance she'll be the first woman to play in the MLB. Wouldn't that be something!
[3] Technically: (+30)+(-80). (See [1] above.)
[4] See above. (What can I say. I love footnotes!)
[5] If: a2+b2=c2, and b=0, then b2=0, so a2+0=c2, which is a2=c2, and that means a=c. (Whew!)