Sonnack.com

But it's a clock!

The main topic this week was how simultaneity is relative to your frame of reference. How there are (virtual) lines of simultaneity where all points on some line — at all distances from you — share the same moment in time. For any instant you pick, that instant — that snapshot — includes all points in your space.

A line of simultaneity freezes the relative positions of objects at a given moment — which enables distance measurements. Simple example: When their watches both read 12 noon, Al and Em were 30 miles apart. A more mathematical example uses x, y, & z (& t), but it amounts to the same thing: a coordinate system.

The gotcha is that simultaneity and coordinate systems are relative when motion is involved!

The goal is a way to accurately describe (map) our frame of reference. We want to assign unique labels — coordinates — to all possible points in space. And time. There are many ways to assign coordinates to space (Euclidean, angular, fractal), but they all rely on the idea of "this point at this moment."

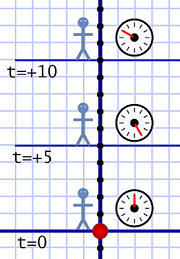Tick marks the snapshot!

So the idea of a simultaneous moment is crucial to being able to map space and time.

Our own position moving through time is one obvious and useful coordinate axis. Once we are marking time, we can also mark space. Time is — as best we know — only one dimension, so we mark it with a single number: "the time!"

Marking space requires a number for each dimension we care about. Our time-space diagrams have only one physical dimension, x, so we only need one number there. (The "real world" is three dimensional, so relativity calculations actually use x, y, & z.)

A word about the 3D world: Our one-dimensional diagrams result in lines of simultaneity. If we're depicting a two-dimensional world (by drawing "3D" with perspective; two dimensions of space, plus one of time — the shorthand is 2+1) there is actually a plane of simultaneity. In real three-dimensional space (3+1), every instant of time has a 3D volume of simultaneity.

Discussions of Special Relativity sometimes use such drawings to illustrate a light cone. The idea is to help you move thinking about one-dimensional time-space diagrams towards thinking about two-dimensional space and, thus, hopefully, to thinking about three-dimensional space.

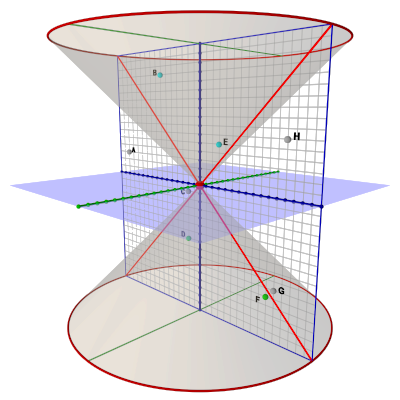The light cone! (More about this another time.)

Other than as a bridge to thinking in three dimensions, two-dimensional diagrams don't add that much (the light cone is pretty, though). The one-dimensional drawings make the point. (Three-dimensional diagrams (plus one of time) aren't really possible, except perhaps with animated video.)

But some 3D thinking is useful with regard to simultaneity. If a 2+1 diagram has a plane of simultaneity (whereas our usual 1+1 diagrams have lines), this says simultaneity is a surface in spacetime. A line is a surface in a two-dimensional diagram. A plane is a surface in a three-dimensional diagram. There's no way to draw it (even in real world 3D), but a volume is a surface in four-dimensional spacetime.

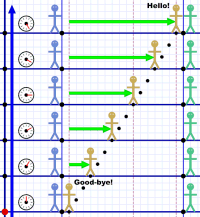Remember this diagram? It should seem pretty quaint to you now!

The point is that each moment is a frozen 3D snapshot of what's happening everywhere at that instant.

The kicker is that, the more they are moving relative to each other, the more Al's snapshots don't look like Em's snapshots (and vice versa).

Since their coordinate systems depend on their individual snapshots, if the snapshots are different, then the coordinate systems are different.

Relative motion warps the coordinate system seen to be in motion. Of course, those at rest with the coordinate system don't see any warping — they see a perfectly normal spacetime system.

This is a good time to remind you of the two basic laws here:

1. The laws of physics are the same for all inertial frames of reference.
2. The speed of light is constant to all frames of reference.

The first one speaks to the Galilean Relativity (or Invariance) known since ancient times. The second one gets us into Special Relativity — the topic of this post series. The point is that the first law is always true. (It turns out, so is the second law.) The laws of physics are the same for all frames of reference.

Light and Time

Light Clock (it weighs a ton)

I haven't discussed it, but you may have heard that "time slows down" when we're moving fast. Per what I just said about the laws of physics, time always runs at the same rate within a frame of reference. But to those outside that frame, time may appear to be running slower.

I'll get more into this in future posts, but for now consider this: Em has a special light clock that measures time by bouncing a light beam up and down (somewhat like a grandfather clock measures time by swinging a pendulum back and forth).

Since she knows how far light travels in the clock (and light travels at a constant speed), she uses this distance to calculate the time. Thus her clock uses the constant speed of light to keep time.

As Em stands there admiring her incredibly accurate timepiece, both she and the clock speed by Al, who is just hanging out. (Or does Al speed past Em? It make no difference.)

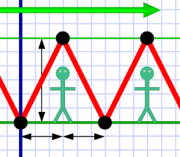Light path is longer to Al!

Al sees the light beam in the clock make a diagonal path as it combines vertical motion in the clock with the horizontal movement of the clock (and Em). To Al, the light travels along a longer path than it does for Em. But since light moves at the same speed for both of them, Al sees Em's clock ticking slower as the light makes the longer journey.

This different perspective of the distance light has to travel is what accounts for the time dilation effect of high-speed travel (seriously high speed).

Summary

We've come a ways in the last three weeks:

1. Constant Motion, Relative Motion, Inertial Frames of Reference.
2. Acceleration changes things (General Relativity!).
3. Galilean Relativity (or Invariance) — ancient stuff.
4. Light Speed is a Constant (c) — game changer.
5. Time-Space diagrams (time goes upwards!).
6. Space-Time Events (a place and a time).
7. Space-Time Coordinate Systems (assigning numbers).
8. Simultaneity Is Relative!
9. Coordinate Systems Are Relative!

Next week I'll dive into the infamous Train Thought Experiments.

There's one with "simultaneous" lightning strikes (you should by now have sense of how that turns out), and one with the weirdest peace treaty signing protocol you ever saw.

My favorite is the one with the train that's too short for the tunnel, yet can be enclosed briefly within the tunnel!

That's what I'll explore next week. More time-space diagrams! But at the end you'll understand what's going on in those situations.

Then we'll take off for a ride through space and time. When we come back, the Earth will have aged much more than we have!