SR #19: "It's Twins!"
 Muon Shower!
Muon Shower!We've covered a great deal of ground in the last four weeks. (Writing a series of posts this long is a new experience for me! I hope you're getting something out of it, too.) We've learned that motion, velocity, simultaneity, and length, are all relative to your frame of reference — motion changes your perception of these things. This week we'll see that time is also relative — motion changes that, too!
So far we only needed a (very imaginary) train to demonstrate the effects of Special Relativity. An Earthly frame of reference was enough to illustrate how motion affects velocity, simultaneity, and length.
But when it comes to time, we're gonna need spaceships!
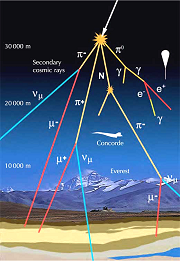
There are places on Earth where relativity affects time.
On the Earth's surface, we detect muons[1] created by cosmic ray collisions in the upper atmosphere.
The problem is that the muons decay into other particles so quickly they should only fly about 450 meters (on average) before decaying.
But due to the energy of the collision, muons fly so fast that their clocks run slower (from our point of view). This gives them time to reach the Earth's surface.
From the muons' point of view, their clocks run normally, and it's the Earth's atmosphere that rushes past them. Therefore they see the distance shortened (just as Em saw the "moving" train tunnel shortened).
From their point of view, they reach the ground because it's not that far to go.
Which is fascinating, but who knows from muons?[2]
Besides, what's more interesting than spaceships and twins?
 No, not The Twins.[4]
No, not The Twins.[4]For the week, our friends Al and Em will be playing the roles of twins.[3]
As always, Em is the traveler (she flies the spaceship), while Al stands his ground on the ground (he has Theories to work on).
The premise is this:
Em flies the spaceship away from Earth to a distance of six light years. We'll assume there's a planet there (let's call it Noether) where Em hangs out for three years. Then she flies back to Earth, to reunite with twin Al.
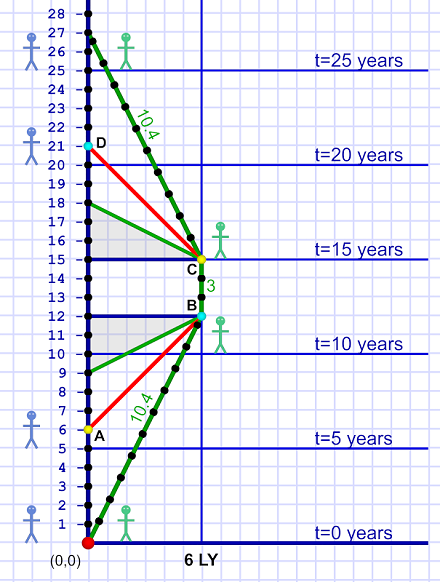
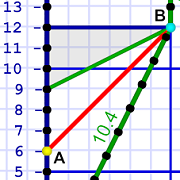
The time-space diagram looks like this:
This diagram packs a number of important features into one image. Also, notice that our diagram scale is very different here. Each spacial (horizontal) unit is now a light-year. That makes each time (vertical) unit a year.
On the left is stay-at-home Al. (Remember the stick figures are just to help keep straight who's on what side. Al's actual position is the vertical world line on the left edge of the diagram.) Once Em leaves (lower left corner), Al hangs out for 27 years (doing Theory stuff).
 Planet Noether
Planet NoetherMeanwhile, Em flies off to planet Noether, which is six light-years away. She flies at 1/2 c — half the speed of light (we can also write c/2).
That means it takes Em's ship — from Al's point of view — 12 years to make the one-way trip (0.5 c × 6 LY = 12 Y).
Yet it turns out that, from Em's point of view, it takes her 10.4 years in the ship (we'll see why later; for now take it as given).
Therefore, Al claims that time is running more slowly for Em. He has aged 12 years while she has aged only 10.4 years.
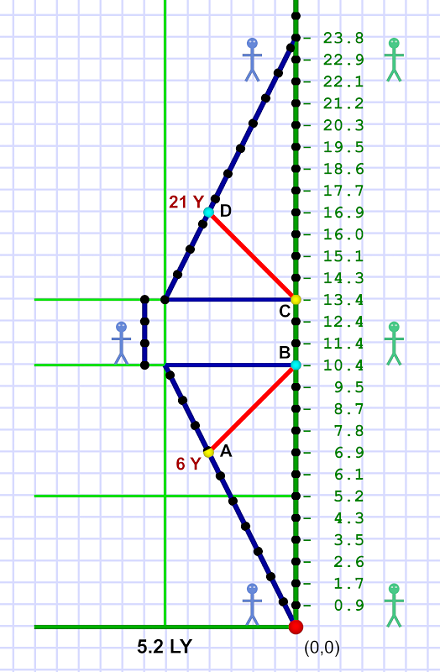
Before we continue, let's take a look at the situation from Em's point of view:
She claims she's standing still while Al, the Earth, and space (!), move past her. And, of course, she thinks her clock is running perfectly normally (and to her, it is).
However, since she sees space moving past at c/2, she sees space foreshortened (just like the muons did). To her, the 6 LY distance the Earth flies seems to be only 5.2 LY.
 Simple Math!
Simple Math!When the planet Noether (which has been traveling along with space) reaches Em, her clock says she's aged 10.4 years. Therefore it makes perfect sense to her that the Earth — moving at half the speed of light — flies 5.2 LY (simple math: 10.4 ÷ 2 = 5.2).
What surprises her (unless she knows about SR) is to see Al's clock on Earth showing it only took him 9 years to make the journey, not the 10.4 years Em has been sitting in the spaceship.
From Em's point of view, time for Al seems to be running slowly! Em sees him age only 9 years to her 10.4 years.
Once again, relativity requires a symmetry between observers in constant motion. We'll explore that symmetry in detail next time. The thing is, Em isn't in constant motion. Once she reaches Noether, she stops (for three years). Then she turns around and returns to Earth.
Both stopping and beginning the return trip are changes of velocity. Remember the diagrams from Dueling Diagrams?
While there is always a symmetry of time and distance with motion, if one party changes their speed or direction, that breaks the perfect symmetry of both points of view being valid.
As mentioned on day two: once acceleration enters the picture, you know whether you're moving or not. So once Em stops at Noether, the symmetry of mutual ignorance is broken, and both observers realize Em was the moving party.
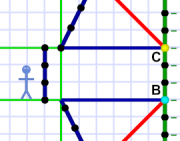 Spacial Discontinuity!
Spacial Discontinuity!Another strange thing Em encounters trying to imagine she's not moving is that when space stops "moving" it's no longer foreshortened.
If Al appears to have traveled 5.2 LY, when he "stops" he is suddenly 6 LY away because with zero speed, zero foreshortening.
So once she stops, the jig is up.
I haven't yet touched on the journey back, and I generally won't spend as much detail on it as I do on the outbound journey. The two legs of the trip are really mirror images of each other, so what's said about one applies to the other (albeit usually in reverse). Suffice for now to say the return trip also takes 10.4 years on Em's clock and 12 on Al's.
 "How was the trip?"
"How was the trip?"There is also the matter of the two laser flashes depicted on the diagrams above. The story is: At his six-year mark (event A) Al sends a message to Em. He knows it takes light six years to make the trip to Noether, so his message should get there (event B) at his twelve-year mark.
Which is just when he predicts Em should arrive (based on her speed of half the speed of light). His message might ask, "How was the trip?"
(Em's reply, of course, takes six years to get back to Al, so he doesn't get a reply to his question until his year 18.)
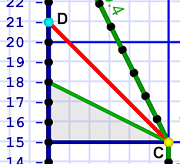 "On my way back!"
"On my way back!"Three years later, when she's about to leave on her return trip, Em sends a message to Al (event C) — probably, "I'm on my way." Naturally that message also takes six years. For now we'll just note that Al receives it at his 21-year mark (event D).
I'll get into all that this week. I'll also get into the importance of those two gray triangles in diagram 1. They're important for understanding what happens, and instrumental once I get to the possibility of FTL.
To end today, if you haven't already done the math, let's compare Al and Em's ages. Al hung around on Earth for 27 years. Em took two 10.4-year spaceship flights. And she hung around on Noether for three years. That's 10.4 + 10.4 + 3 = 23.8.
Em is now 3.2 years younger than her twin, Al!
Stay tuned for details!
[1] About 10,000 per minute per square meter! The Moon creates a muon shadow as it blocks the interstellar sky.
[2] For the record: Muons are second-family cousins to the common electron. As with all second- or third-family particles, they're too massive to hang around long. Muons normally decay in two microseconds or so.
[3] In point of fact, they were born only three years apart, both in March. Completely different families, of course, but it was all well over 100 years ago, so close enough for our purposes.
[4] I'm not ready to talk about them, yet. [frowny face]