SR #22: Relative Time
 Fantastic stuff, right?
Fantastic stuff, right?Last time we saw that Em non-paradoxically time-travels over three years into Al's future by flying 12 light years at half the speed of light for just over two decades. Her journey completed, Em has aged only 20.8 years while Al has aged 24.
That may not seem like much of a gain, but Em was only moving really fast — not really, really fast. If she travels at 99% of light-speed, her round trip shortens to 1.7 years while Al doesn't wait much longer than it takes light to make the six light-year round trip: 12.12 years! And at 99.9% c, Em's whole trip takes her only half a year!
Today we break down dime tilation. I mean, time dilation!
By "break down" I mean provide some charts and talk about it some more. Mainly about why time has to slow down when you look at a moving frame.
Let's start with the charts:
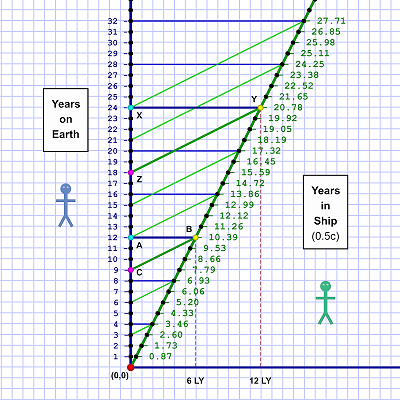
The first one is a time-space diagram of Em's flight (at c/2 as usual) from Al's point of view and the years that elapse. For these diagrams we assume Em flies continuously and does not stop.
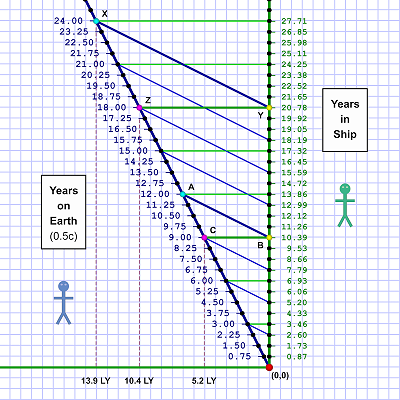
The second one is the same thing from Em's point of view. Remember that she sees space as moving and therefore contracted — that's why the marked distances are less.
By the way: The scale of diagram 2 sets each square at 0.866 rather than 1.0. That doesn't change anything, it just lets the diagram lines live neatly on the graph paper lines. Think of it as a zoom.
Certain reference events are marked on each chart to show how things shift due to the frame of reference change. For example, notice that events A & B are simultaneous to Al (diagram 1), but B & C are simultaneous to Em (diagram 2).
Are you're wondering what Em's chart would look like if her years were sliced in whole years (1, 2, 3,…) like Al's are in his chart? It'd look like a mirror image of Al's chart — same numbers.
The numbers are based on the gamma factor for moving at 0.5 c (aka c/2). At that speed, the gamma (γ) is 0.866. It's how much the length contracts and time dilates (expands) — 86.6%!
Which may have you wondering, what is the gamma at different speeds?
| %c | m/s | MPH | gamma | 1/gamma |
|---|---|---|---|---|
| 0.0000 | 0 | 0 | 1.00000000 | 1.00000000 |
| 0.0001 | 300 | 671 | 1.00000000 | 1.00000000 |
| 0.0010 | 2,998 | 6,706 | 1.00000000 | 1.00000000 |
| 0.0100 | 29,979 | 67,062 | 1.00000001 | 0.99999999 |
| 0.1000 | 299,792 | 670,616 | 1.00000050 | 0.99999950 |
| 1.0000 | 2,997,925 | 6,706,164 | 1.00005000 | 0.99995000 |
| 10.0000 | 29,979,246 | 67,061,642 | 1.00503782 | 0.99498744 |
| 20.0000 | 59,958,492 | 134,123,284 | 1.02062073 | 0.97979590 |
| 25.0000 | 74,948,114 | 167,654,105 | 1.03279556 | 0.96824584 |
| 30.0000 | 89,937,737 | 201,184,927 | 1.04828484 | 0.95393920 |
| 33.3333 | 99,930,719 | 223,538,584 | 1.06066004 | 0.94280916 |
| 40.0000 | 119,916,983 | 268,246,569 | 1.09108945 | 0.91651514 |
| 50.0000 | 149,896,229 | 335,308,211 | 1.15470054 | 0.86602540 |
| 60.0000 | 179,875,475 | 402,369,853 | 1.25000000 | 0.80000000 |
| 66.6666 | 199,861,439 | 447,077,168 | 1.34163971 | 0.74535659 |
| 70.0000 | 209,854,721 | 469,431,495 | 1.40028008 | 0.71414284 |
| 75.0000 | 224,844,344 | 502,962,316 | 1.51185789 | 0.66143783 |
| 80.0000 | 239,833,966 | 536,493,138 | 1.66666667 | 0.60000000 |
| 85.0000 | 254,823,589 | 570,023,959 | 1.89831599 | 0.52678269 |
| 90.0000 | 269,813,212 | 603,554,780 | 2.29415734 | 0.43588989 |
| 91.0000 | 272,811,137 | 610,260,944 | 2.41191535 | 0.41460825 |
| 92.0000 | 275,809,061 | 616,967,108 | 2.55155182 | 0.39191836 |
| 93.0000 | 278,806,986 | 623,673,272 | 2.72064781 | 0.36755952 |
| 94.0000 | 281,804,911 | 630,379,437 | 2.93105191 | 0.34117444 |
| 95.0000 | 284,802,835 | 637,085,601 | 3.20256308 | 0.31224990 |
| 96.0000 | 287,800,760 | 643,791,765 | 3.57142857 | 0.28000000 |
| 97.0000 | 290,798,684 | 650,497,929 | 4.11345035 | 0.24310492 |
| 98.0000 | 293,796,609 | 657,204,093 | 5.02518908 | 0.19899749 |
| 99.0000 | 296,794,533 | 663,910,258 | 7.08881205 | 0.14106736 |
| 99.5000 | 298,293,496 | 667,263,340 | 10.01252349 | 0.09987492 |
| 99.9000 | 299,492,666 | 669,945,805 | 22.36627204 | 0.04471018 |
| 99.9900 | 299,762,479 | 670,549,360 | 70.71244595 | 0.01414178 |
| 99.9990 | 299,789,460 | 670,609,716 | 223.60735677 | 0.00447212 |
| 99.9999 | 299,792,158 | 670,615,751 | 707.10695797 | 0.00141421 |
| %c | m/s | MPH | gamma | 1/gamma |
Wonder no more! (If it isn't obvious, this is sort of a reference post.)
This table is handy for those who are curious about how much things change at different speeds, but don't want to tackle the gamma factor equation I showed you recently.
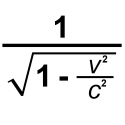 The gamma factor.
The gamma factor.Notice that the table isn't linear — the first and last rows break speed into much smaller increments. That's because those are the most interesting parts!
The gamma isn't even noticeable until at least one-hundredth of one percent of the speed of light (which is still a bodacious 67 thousand MPH). And at that speed gamma amounts to a change of just ten-billionths!
At the next notch up, a mere one-tenth of one percent of c (a hefty 670 thousand MPH), gamma is still only half of one-millionth. It's really not until around 10% of c (a whopping 67 million MPH) that gamma really becomes noticeable.
 99% squeeze: not noticeable.
99% squeeze: not noticeable.If you look at the right column (1/gamma), that shows the amount of length contraction, so things are still 99% of their natural length at 10% of the speed of light! It's also the amount of time reduction, so Em's clock at that speed (which is millions of MPH) runs only 99% slower according to Al.
From Em's point of view gamma says how much Al's clock is running faster, so according to her his clock is running 1.005 times faster. Still not a lot happening at one-tenth light speed!
Even at half the speed of light (as we've seen for weeks), the effect isn't huge. Em's clock and length seem only 86% reduced to Al. As we've seen, that gives a ratio of 10.4 years for her to his 12.
 50% squeeze: way noticeable!
50% squeeze: way noticeable!We need to get to 90% of the speed of light before gamma reaches even two (it actually reaches it — not ironically — at 86.6%). But now things really start to heat up (you'll notice nearly the entire bottom third of the table involves speeds in the 90% range)!
At 99% of c the gamma is just over seven, and at 99.5% it's just over ten!
At 99.9% it's up to 22+, and at 99.99% it skyrockets to 70 (and some change). One more decimal place — 99.999% — and now gamma is well over two hundred. (And notice how extreme length and time contraction have gotten.)
§ § §
 Simple Math
Simple MathAt the beginning I said that Em's 12 LY trip at 99% of c only takes her 1.7 years and only half a year at 99.9% (and that Al's time converged on the round-trip time for light: 12 years).
Let's work the first one through. We'll do it from Al's perspective and from Em's.
Al sees Em make a 12 LY journey at 0.99 c. The fundamental motion equation is d = vt (where d is time, v is velocity, and t is time — 60 MPH, v, times 2 hours, t, equals 120 miles, d).
Here I have v (0.99 c) and d (12 LY); I need t!
I get that with d/v = t (120 miles ÷ 60 MPH = 2 hours). So Al sees Em taking (12 ÷ 0.99 =) 12.12 years to make the trip. He knows her clock runs slow; the chart tells him it runs 0.141 times slower. What seems 12.12 years to Al will seem like 1.7 years to Em.
 Baseball field if you passed it with a gamma of about 10 (in other words, at 99.5% c).
Baseball field if you passed it with a gamma of about 10 (in other words, at 99.5% c).From Em's point of view, space (and Al) is moving at 0.99 c, so it suffers extreme foreshortening —the same 0.141 factor. So that 12 LY now looks like 1.69 LY!
We have d (1.69) and v (same 0.99) again, so 1.69 ÷ 0.99 = 1.7 years. Em sees her time interval ending up the same length Al does — a bit under two years.
I'll leave the math for what happens at 99.9% of light speed as an exercise for the interested reader.
§ § §
Tomorrow is Friday, and in this series I like to discuss topics closely related to light on Fridays. It's the International Year of Light, for one thing, and obviously light has everything to do with Special Relativity.
In the next post I'll pick up a thread I started two Fridays ago and talk about light clocks (yes, I know, a heavy subject). They're the reason time dilation has to occur.
Length contraction can be hard to wrap your head around, but there turns out to be a simple basis for time dilation, a simple reason Al has to see Em's clock running slower.
Funny thing is, it was one of the first SR things I read about back in high school. It took me years for the light bulb to finally go on about it, but I can be as slow as anyone on the uptake.
Hopefully I can explain it in a way where it won't take years for your light bulbs to light!
We're almost done! (Which is to say, I'm almost out of diagrams.) Light clocks to end the week, and some final thoughts next week, and I'll call it a series.
(Besides, it's getting nice out here, and baseball is in full swing now, and I don't know about you, but I'm really tired of thinking — let alone writing — about Special Rela-friggin'-tivity!)