Sonnack.com

A really big time machine!

This week I've focused on the relativity of time under motion, and we've seen that moving very fast allows "time travel" into the future. Very handy if you don't mind the one-way trip. What's more, a spaceship capable of such a flight is physically possible, so it's a "time machine" we know works!

On Monday I described how fast-moving, but short-lived, muons created high in the atmosphere live long enough to reach the ground due to time dilation. That's just one place we see Special Relativity actually working exactly as Einstein described. For another, fast-moving particles at CERN have decay times showing they, too, have slow clocks.

As we'll see today, light's behavior requires time appear to run slower!

(Imaginary) light clock.

Of course, that's true of all of Special Relativity — that light moves at a constant speed to all observers is the basis of SR.^[1]

But the connection light's speed has with time dilation seems more direct here than how it affects length (or energy or mass — which I haven't discussed). The connection with simultaneity is more direct, but the concept of lines of simultaneity is still a bit abstract.

That time appears to run slower is very concrete, and its physical basis seems almost obvious once the idea clicks.^[2]

Some texts on SR more or less start with this (but it does require being clear about the speed of light's consistency and what that implies — I really wasn't).

What I'm talking about here is the idea of a light clock.

As a general rule, any clock works by ticking. That is, any clock works by having something that goes "back and forth" (for some useful definition of "back and forth"). A grandfather clock, for example, usually has a pendulum that swings back and forth.

Clock escapement.

If you've ever taken a watch or smaller clock apart, you know the gear train starts with what's called an escapement — often a little curved, clawed bar that ticks back and forth.

Its movement creates the ticking sound clocks make as it slices the pressure of the spring into moments the watch ticks off.

Electronic clocks use a vibrating crystal (remember "quartz clocks"?) that does the ticking. These crystals vibrate at extremely high rates of speed, and are very stable in holding the rate constant. As such they make for very accurate clocks.

Cheaper clocks that plug into the mains use the alternating current (A.C.) as their ticking. In the USA, the mains "ticks" 60 times per second, which is convenient. (In other parts of the world, 50 cycles per second is common.)

Watch quartz crystal.

What if we made a clock using the most accurate, most consistent, fastest thing we know: light!

If we bounce light back and forth over a known distance, we can consider each trip across that distance a "tick" of some extremely fast pendulum (it probably just goes "tck" or even "tk").

You'll recall^[3] that light travels about one meter in three nanoseconds. If we bounce light back and forth over a one-meter distance, then each tick is three nanoseconds. When we slice time this finely, we end up with a very accurate clock.

So far, so good.

Now let's imagine our clock bounces light up and down vertically. For us to use the clock in our own frame of reference, it can bounce light any which way. There is no preferred orientation for us.

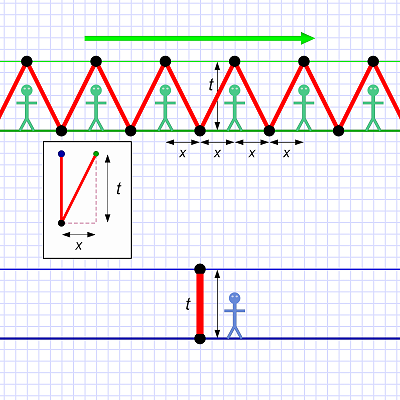
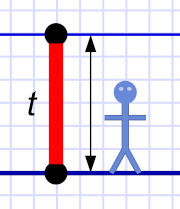Diagram 1. Al's clock.

But to illustrate what happens when motion is involved we'll use up and down because that's where we'll see the effect of time dilation.

Em is our usual traveler, so we'll haul one of these clocks onto her spaceship. She'll fly past Al to see what happens.

Meanwhile, Al has a clock of his own so they can compare notes. Diagram 1 shows Al and his clock.

Note that this is not a time-space diagram, but a flat (schematic) drawing of Al with his light clock beam bouncing up and down.

The t indicates the time it takes for one tick of Al's tclock.

The question for Al is what does Em's clock look like from his point of view as she speeds past. Remember that, to Em, her own clock looks just like Al's does to him in diagram 1. Her light clock bounces light straight up and down, just like his.

But what Al sees as Em passes by looks like this:

Diagram 2. Al watches Em (and her clock) pass by.

Al sees Em's clock bouncing light up and down (as she does), but he also sees the light having to take a longer path because the clock is moving!

Em's clock moves some amount (x) during each tick, so the light not only has to make the vertical distance, it has to cover some horizontal distance as well. (But this is relative only to Al! Em sees her clock normally.)

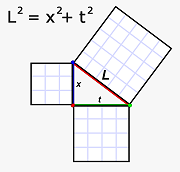Pythagoras' pretty Theory!

Maybe you recall the post where Pythagorean Theory entered into calculations for physical motion that wasn't along the line of travel.

When Em threw the ball upwards (or dropped it), the slanted path — again covering both vertical and horizontal distance — required Pythagoras to tell us the total distance.

This is the same situation. From Al's perspective, the light in Em's clock has to travel vertical and horizontal distance, so he uses Pythagoras to determine the total length the light travels in her clock.

What matters is that the total distance in Em's clock is always longer than in his. It has to be. Adding any amount of horizontal distance has to make the total distance greater. Basic geometry.

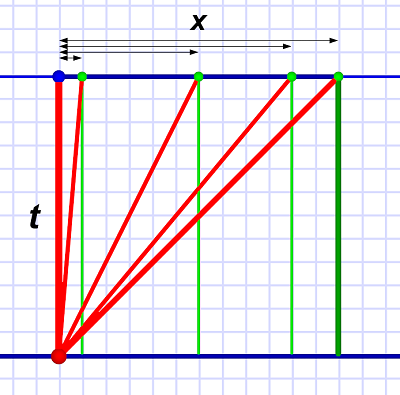Diagram 3. The length Al sees the light in Em's clock travel depends on Em's speed relative to him. The greatest angle (45°) is at light speed; the minimum angle (0°, straight up and down) is at zero. Depicted above (left to right) are: 0 c, 1/12 c, 1/2 c, 5/6 c and c.

But here's the kicker!

Remember: Light always travels at the same speed to all observers!

So if a tick in Al's clock is just the distance t, but he sees the distance in Em's clock as t+x (for any x other than zero), then Em's ticks have to be longer.

If the speed of light is constant (which it is), and if — from Al's point of view — the light in Em's clock takes longer to "tick" (which it does), then Al has to see Em's clock as running slower.

It's the only possible conclusion.

Sorry, looks like there won't be much going forth boldly and exploring strange new worlds. At least not at warp speed.

What's interesting is that the geometry in diagram 3 leads directly the Lorentz equations we've been using to determine gamma. Special Relativity is a geometrical theory that only requires Pythagorean math. (General Relativity is a whole other kettle of tensors.)

On that note, we're essentially done!

The last posts in this series will use what I've shown you so far to explain why FTL is almost certainly forever an impossibility — even in principle.

Suffice to say a new Einstein would have to come along and change our notions of reality just as Einstein did and as Newton did before him.